题目内容
6.如图1,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,沿折线B→C→D→A运动,点P运动的速度为2个单位长度/秒,设点P运动的时间为x秒,△ABP的面积为y,若y关于x的函数图象如图2所示,则M点的纵坐标为48.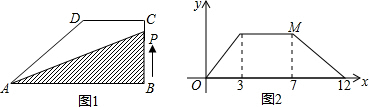
分析 根据题意,分析P的运动路线,分2个阶段分别讨论,可分别得处DC、BC和AD的值,得出三角形的面积,再得出点M的坐标即可.
解答 解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;
且不变的面积是在x=3,x=7之间;
可知当x=3时,点P恰好到点C处,
当x=7时,点P恰好到点D处,
此时P点运动3秒,即BC=6;
同理可得CD=8,AD=10,
过点D作DN⊥AB于点N,则有DN=BC=6,BN=CD=8,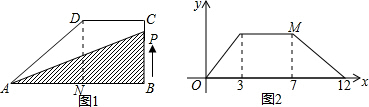
在Rt△ADN中,AN=$\sqrt{A{D}^{2}-D{N}^{2}}$=8,
所以AB=BN+AN=8+8=16,
所以△ABC的面积为 $\frac{1}{2}$AB•BC=$\frac{1}{2}$×16×6=48,
所以可得点M的坐标为(7,48)
故答案为:48
点评 本题主要考查了动点问题的函数图象问题与三角形面积的求法等知识点,要求学生能够要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
相关题目
 按要求作图,并标出位置.
按要求作图,并标出位置.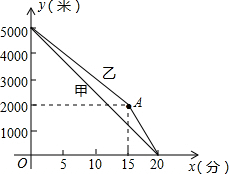 甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题: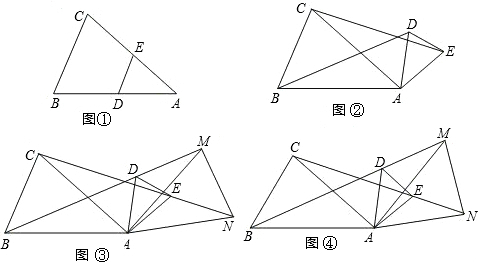
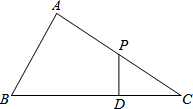 如图,△ABC中,∠A=90°,P是AC的中点,PD⊥BC于D,BC=9,CD=3,求AB.
如图,△ABC中,∠A=90°,P是AC的中点,PD⊥BC于D,BC=9,CD=3,求AB.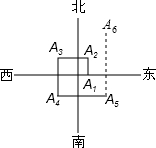 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )