题目内容
(Ⅰ)解方程组:
;
(Ⅱ)解不等式组:
.
|
(Ⅱ)解不等式组:
|
考点:解二元一次方程组,解一元一次不等式组
专题:计算题
分析:(Ⅰ)方程组整理后,利用加减消元法求出解即可;
(Ⅱ)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
(Ⅱ)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答:解:(Ⅰ)方程组整理得:
,
由②得:x=3y+18,
代入①得:8(3y+18)=12,
解得:y=-4,
将y=-4代入得:x=-12+18=6,
则方程组的解为
;
(Ⅱ)不等式整理得:
,
由①得:x≤1;由②得:x<4,
则不等式组的解集为x≤1.
|
由②得:x=3y+18,
代入①得:8(3y+18)=12,
解得:y=-4,
将y=-4代入得:x=-12+18=6,
则方程组的解为
|
(Ⅱ)不等式整理得:
|
由①得:x≤1;由②得:x<4,
则不等式组的解集为x≤1.
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,在等边△ABC中,D,E分别AC,AB是上的点,且AD=BE,CE与BD交于点P,则∠BPE的度数为( )
如图,在等边△ABC中,D,E分别AC,AB是上的点,且AD=BE,CE与BD交于点P,则∠BPE的度数为( )| A、75° | B、60° |
| C、55° | D、45° |
 (1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2.
(1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2.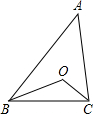 如图,已知点O是△ABC的两条角平分线的交点.
如图,已知点O是△ABC的两条角平分线的交点. 如图,已知a∥b,∠1=50°,则∠2的度数为
如图,已知a∥b,∠1=50°,则∠2的度数为