题目内容
（1）先化简，再求值：（a-2）（a+2）+3（a+2）2-6a（a+2），其中a=2．（2）如图，已知∠1=∠2，∠B=∠C，请说明AB∥CD．
考点：平行线的判定,整式的混合运算—化简求值
专题：
分析：（1）先根据整式混合运算的法则把原式进行化简，再把a=2代入进行计算即可；
（2）先根据∠1=∠2，∠1=∠4得出∠2=∠4，故EC∥BF，由平行线的性质得出∠C=∠3，故可得出∠B=∠3，所以AB∥CD．
（2）先根据∠1=∠2，∠1=∠4得出∠2=∠4，故EC∥BF，由平行线的性质得出∠C=∠3，故可得出∠B=∠3，所以AB∥CD．
解答：
解：（1）原式=（a2-4）+3（a2+4a+4）-（6a2+12a）
=-2a2+8，
当a=2时，原式=-2×22+8=0；
（2）∵∠1=∠2，∠1=∠4，
∴∠2=∠4，
∴EC∥BF，
∴∠C=∠3，
∵∠B=∠C，
∴∠B=∠3，
∴AB∥CD．
解：（1）原式=（a2-4）+3（a2+4a+4）-（6a2+12a）=-2a2+8，
当a=2时，原式=-2×22+8=0；
（2）∵∠1=∠2，∠1=∠4，
∴∠2=∠4，
∴EC∥BF，
∴∠C=∠3，
∵∠B=∠C，
∴∠B=∠3，
∴AB∥CD．
点评：本题考查的是平行线的判定，用到的知识点为：内错角相等，两直线平行．
练习册系列答案
名校课堂系列答案
相关题目
抛物线y=（x-2）2+3的顶点坐标是（ ）
| A、（2，3） |
| B、（-2，3） |
| C、（2，-3） |
| D、（-2，-3） |
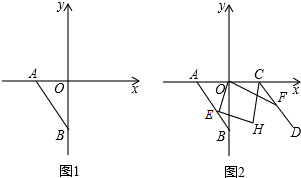
如图，已知四边形ABCD的顶点坐标分别为A（4，1），B（5，3），C（4，5），D（2，3）．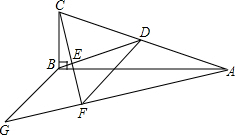
如图，在△ABC中，∠ABC=90°，D为AC的中点，过点C作CE⊥BD于点E，作∠GAB=∠CAB，CE的延长线与AG交于点F，点G在AF的延长线上，且FG=BD，连结BG、DF