题目内容
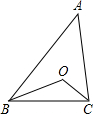 如图,已知点O是△ABC的两条角平分线的交点.
如图,已知点O是△ABC的两条角平分线的交点.(1)若∠A=30°,则∠BOC的大小是
(2)若∠A=60°,则∠BOC=的大小是
(3)若∠A=80°,则∠BOC的大小是
(4)若∠A=n°,猜想∠BOC的大小,并用所学过的知识说明理由.
考点:三角形内角和定理
专题:探究型
分析:先列出∠A、∠ABC、∠ACB的关系,再列出∠BOC、∠OBC、∠OCB的关系,然后列出∠ABC和∠OBC、∠ACB和∠OCB的关系,问题得解.
解答:解:∠BOC=
∠A+90°.
∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+
∠ABC+
∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=
∠A+90°,
∴若∠A=n°,∠BOC=
n°+90°,
由此可得问题(1),(2),(3),(4)的答案,
故答案为:105°,120°,130°.
| 1 |
| 2 |
∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+
| 1 |
| 2 |
| 1 |
| 2 |
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=
| 1 |
| 2 |
∴若∠A=n°,∠BOC=
| 1 |
| 2 |
由此可得问题(1),(2),(3),(4)的答案,
故答案为:105°,120°,130°.
点评:本题考查了三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件以及三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
相关题目
 如图,已知四边形ABCD的顶点坐标分别为A(4,1),B(5,3),C(4,5),D(2,3).
如图,已知四边形ABCD的顶点坐标分别为A(4,1),B(5,3),C(4,5),D(2,3).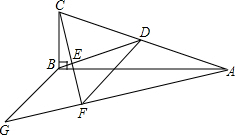 如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF
如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF