题目内容
11.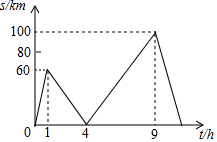 A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②乙出发4h后追上甲;
③甲比乙晚到$\frac{5}{3}$h;
④甲车行驶8h或9$\frac{1}{3}$h,甲,乙两车相距80km;
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据函数图象即可得到甲车行驶的速度以及乙车行驶的速度;根据函数图象即可得到乙出发4h后追上甲;根据图象,当乙到达B地时,甲乙相距100km,据此可得甲比乙晚到$\frac{5}{3}$h;根据甲,乙两车相距80km,列出方程进行求解即可.
解答 解:①由图可得,甲车行驶的速度是60÷1=60km/h,
∵甲先出发1h,乙出发3h后追上甲,
∴3(v乙-60)=60,
∴v乙=80km/h,
即乙车行驶的速度是80km/h,故①正确;
②∵当t=1时,乙出发,当t=4时,乙追上甲,
∴乙出发3h后追上甲,故②错误;
③由图可得,当乙到达B地时,甲乙相距100km,
∴甲比乙晚到100÷60=$\frac{5}{3}$h,故③正确;
④由图可得,当60t+80=80(t+1)时,
解得t=8;
当60t+80=640时,
解得t=9$\frac{1}{3}$,
∴甲车行驶8h或9$\frac{1}{3}$h,甲,乙两车相距80km,故④正确;
综上所述,正确的个数是3个.
故选:C.
点评 本题主要考查了一次函数的应用,解决问题的关键是根据函数图象获得关键的信息,利用行程问题的数量关系列式计算.

练习册系列答案
相关题目
6.线段a,b,c的长度比为1:$\sqrt{2}$:1,若以a,b,c为边组成三角形,则三角形的形状是( )
| A. | 等腰三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 无法组成三角形 |
16.一次函数y=k1x+b1的图象与y=k2x+b2的图象相交于点P(-2,3),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{b=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$ |
3.已知直线y=kx+b(kb≠0)不经过第二象限,则下列结论正确的是( )
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k<0,b<0 | D. | k>0,b<0 |
18.计算(x+2)2(x-2)2的结果是( )
| A. | x2-16 | B. | x4+8x2+16 | C. | x4-8x2+16 | D. | x4+16 |