题目内容
1．解不等式组：$\left\{\begin{array}{l}{2x+1＞-1}\\{\frac{2x+1}{3}≥x-1}\end{array}\right.$，并把不等式组的解集在数轴上表示出来．分析 根据解一元一次不等式组的方法可以解答本题并把不等式的解集在数轴上表示出来．
解答 解：$\left\{\begin{array}{l}{2x+1＞-1}&{①}\\{\frac{2x+1}{3}≥x-1}&{②}\end{array}\right.$，
由不等式①，得x＞-1，
由不等式②，得x≤4，
∴原不等式组的解集是-1＜x≤4，在数轴上表示如下图所示，
．
点评 本题考查解一元一次不等式组，解答本题的关键是明确解一元一次不等式的方法．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
11．
如图，直线y=ax+b过点A（0，3）和点B（-2，0），则方程ax+b=0的是（ ）
如图，直线y=ax+b过点A（0，3）和点B（-2，0），则方程ax+b=0的是（ ）| A． | x=3 | B． | x=0 | C． | x=-2 | D． | x=-3 |
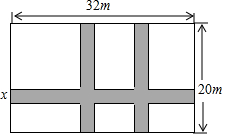如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2，则道路宽x为1m．
6．若正比例函数的图象经过点（2，-3），则这个图象必经过点（ ）
| A． | （-3，-2） | B． | （2，3） | C． | （3，-2） | D． | （-4，6） |
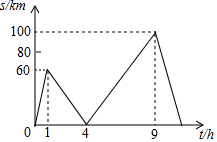A，B两地相距640km，甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s（km），甲行驶的时间为t（h），s与t的关系如图所示，下列说法：