题目内容
15．一列火车甲匀速行驶，经过一座铁路桥，轿头有一根石柱，石柱上记载着桥的修建情况，火车甲经过这根石柱用了15s．桥上还有一列长300m的火车乙因为让道而停在轿上，火车甲经过这列300m长的火车乙用了25s，设火车甲长xm．（1）火车甲经过石柱所行驶的路程是x，则火车甲的速度可表示为$\frac{x}{15}$．
（2）火车甲经过300m长的火车乙所行驶的路程是300m，则火车甲的速度可表示为$\frac{300}{25}$．
（3）根据速度相等，列方程得$\frac{x}{15}$=$\frac{300}{25}$，把方程左右两边变成乘法得25x=15×300，解得x=180．
分析 （1）（2）火车甲经过石柱所行驶的路程是火车的长度，经过这列300m长的火车行驶的路程是300m，进一步利用路程除以时间求得速度即可；
（3）都表示火车的速度，由此联立方程求得答案即可．
解答 解：（1）火车甲经过石柱所行驶的路程是x，则火车甲的速度可表示为$\frac{x}{15}$．
（2）火车甲经过300m长的火车乙所行驶的路程是300m，则火车甲的速度可表示为$\frac{300}{25}$．
（3）根据速度相等，列方程得$\frac{x}{15}$=$\frac{300}{25}$，把方程左右两边变成乘法得25x=15×300，解得x=180．
故答案为：x，$\frac{x}{15}$；300m，$\frac{300}{25}$；$\frac{x}{15}$=$\frac{300}{25}$，25x=15×300，x=180．
点评 此题考查一元一次方程的实际运用，掌握路程、速度、时间之间的数量关系是解决问题的关键．
练习册系列答案
相关题目
3．下列化去根号内分母的变形中，正确的是（ ）
| A． | $\sqrt{3\frac{1}{4}}$=2$\sqrt{13}$ | B． | $\sqrt{\frac{2m}{3n}}$=3n$\sqrt{6mn}$ | ||
| C． | $\sqrt{\frac{a}{{b}^{2}}+\frac{b}{{a}^{2}}}$=（$\frac{1}{a}$+$\frac{1}{b}$）$\sqrt{a+b}$ | D． | $\sqrt{\frac{2{x}^{2}}{27（x-1）^{2}}}$=$\frac{x}{9（x-1）}$$\sqrt{6}$（x＞1） |
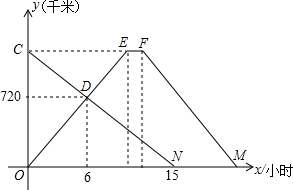快车甲和慢车乙分别从A、B两站同时出发，相向而行．快车到达B站后，停留1小时，然后原路原速返回A站，慢车到达A站即停运休息．如图表示的是两车离A站的距离y（千米）与行驶时间x（小时）的函数图象．请结合图象信息，解答下列问题：