题目内容
4.在平面直角坐标系中,点P的坐标为(0,-5),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于y轴,且AB=8,反比例函数y=$\frac{k}{x}$(k≠0)经过点B,则k=-8或-32.分析 设AB交y轴于点C,利用垂径定理可求得PC的长,则可求得B点坐标,代入反比例函数解析式可求得k的值.
解答 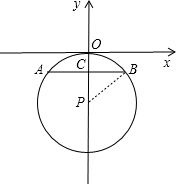 解:
解:
设线段AB交y轴于点C,当点C在点P的上方时,连接PB,如图,
∵⊙P与x轴相切,且P(0,-5),
∴PB=PO=5,
∵AB=8,
∴BC=4,
在Rt△PBC中,由勾股定理可得PC=$\sqrt{P{B}^{2}-B{C}^{2}}$=3,
∴OC=OP-PC=5-3=2,
∴B点坐标为(4,-2),
∵反比例函数y=$\frac{k}{x}$(k≠0)经过点B,
∴k=4×(-2)=-8;
当点C在点P下方时,同理可求得PC=3,则OC=OP+PC=8,
∴B(4,-8),
∴k=4×(-8)=-32;
综上可知k的值为-8或-32,
故答案为:-8或-32.
点评 本题主要考查切线的性质及反比例函数图象上点的坐标特征,利用垂径定理和切线的性质求得PC的长是解题的关键,注意分两种情况.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
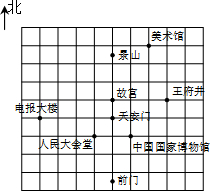 “四个一”活动自2014年9月启动至今,北京市已有60万中小学生参观了天安门广场的升旗仪式.下图是利用平面直角坐标系画出的天安门广场周围的景点分布示意图.如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示故宫的点的坐标为(0,1),表示中国国家博物馆的点的坐标为(1,-1),那么表示人民大会堂的点的坐标是(-1,1).
“四个一”活动自2014年9月启动至今,北京市已有60万中小学生参观了天安门广场的升旗仪式.下图是利用平面直角坐标系画出的天安门广场周围的景点分布示意图.如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示故宫的点的坐标为(0,1),表示中国国家博物馆的点的坐标为(1,-1),那么表示人民大会堂的点的坐标是(-1,1).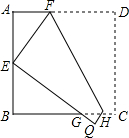 如图,将边长为6cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是$\frac{9}{4}$cm.
如图,将边长为6cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是$\frac{9}{4}$cm. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则斜边AB=2$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则斜边AB=2$\sqrt{3}$.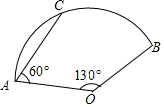 如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则$\widehat{BC}$的长为$\frac{7}{3}$π.
如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则$\widehat{BC}$的长为$\frac{7}{3}$π.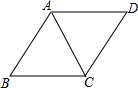 如图,菱形ABCD的边长为5,sinB=0.8,则对角线AC的长为2$\sqrt{5}$.
如图,菱形ABCD的边长为5,sinB=0.8,则对角线AC的长为2$\sqrt{5}$.