题目内容
14.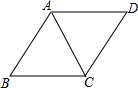 如图,菱形ABCD的边长为5,sinB=0.8,则对角线AC的长为2$\sqrt{5}$.
如图,菱形ABCD的边长为5,sinB=0.8,则对角线AC的长为2$\sqrt{5}$.
分析 过C作CE⊥AB于E,则∠CEB=∠CEA=90°,解直角三角形求出EC,根据勾股定理求出BE,求出AE,根据勾股定理求出AC即可.
解答 解: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=5cm,
过C作CE⊥AB于E,则∠CEB=∠CEA=90°,
∵sinB=$\frac{CE}{BC}$=0.8,BC=5cm,
∴BE=4cm,
在Rt△BEC中,由勾股定理得BE=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
∴AE=5cm-3cm=2cm,
在Rt△CEA中,由勾股定理得:AC=$\sqrt{C{E}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2 $\sqrt{5}$(cm),
故答案为:2 $\sqrt{5}$.
点评 本题考查了菱形的性质,勾股定理,解直角三角形的应用,能构造直角三角形是解此题的关键,注意:菱形的四条边都相等.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
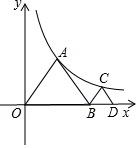 如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).
如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).