题目内容
19．
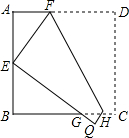如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是$\frac{9}{4}$cm．
分析 设EF=FD=x，在RT△AEF中利用勾股定理即可解决问题．
解答 解：如图：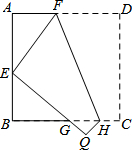
∵四边形ABCD是正方形，
∴AB=BC=CD=AD=6，
∵AE=EB=3，EF=FD，设EF=DF=x．则AF=6-x，
在RT△AEF中，∵AE2+AF2=EF2，
∴32+（6-x）2=x2，
∴x=$\frac{15}{4}$，
∴AF=6-$\frac{15}{4}$=$\frac{9}{4}$cm，
故答案为$\frac{9}{4}$．
点评 本题考查翻折变换、正方形的性质、勾股定理等知识，解题的关键是设未知数利用勾股定理列出方程解决问题，属于中考常考题型．
练习册系列答案
相关题目
在平面直角坐标系xOy中，一次函数y=kx和y=-x+3的图象如图所示，则关于x的一元一次不等式kx＜-x+3的解集是x＜1．
如图，一把长方形直尺沿直线断开并错位，点E，D，B，F在同一条直线上．如果∠ADE=126°，那么∠DBC=54°．