题目内容
17．若$\frac{（a+3）x}{（3-2a）（x-1）}$=$\frac{x}{1-x}$成立，则a应取何值？分析 根据分式的分子分母都乘以或除以同一个不为零的数或者整式，分式的值不变，可得答案．
解答 解：由若$\frac{（a+3）x}{（3-2a）（x-1）}$=$\frac{x}{1-x}$成立，得
（a+3）+（3-2a）=0．
解得a=6，
若$\frac{（a+3）x}{（3-2a）（x-1）}$=$\frac{x}{1-x}$成立，a应取6．
点评 本题考查了分式的基本性质，分式的分子分母都乘以或除以同一个不为零的数或者整式，分式的值不变．
练习册系列答案
相关题目
7．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | B． | $\frac{0.2a+b}{a+0.2b}$=$\frac{2a+b}{a+2b}$ | ||
| C． | -$\frac{x+1}{x-y}$=$\frac{x-1}{x-y}$ | D． | $\frac{x-\frac{1}{2}y}{\frac{1}{2}x+y}$=$\frac{2x-y}{x+2y}$ |
8．底面半径R，高为h的圆柱与底面半径为r，高为h的圆柱的体积的比是9：25，则R：r等于（ ）
| A． | 9：25 | B． | 25：9 | C． | 3：5 | D． | 5：3 |
9．若（x-2z）2+|2x-1|+|y+3|=0，则满足等式的x、y、z分别是（ ）
| A． | x=$\frac{1}{2}$，y=3，z=1 | B． | x=-$\frac{1}{2}$，y=-3，z=-1 | C． | x=$\frac{1}{2}$，y=-3，z=$\frac{1}{4}$ | D． | x=$\frac{1}{2}$，y=3，z=2 |
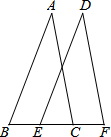已知：如图，∠B=∠DEF，∠ACB=∠F，BE=CF．求证：AB=DE．
列方程解应用题：如图，在长为32m，宽为20m的矩形地面上，修筑同样宽的两条平行且与另一条相互垂直的道路，余下的六个空白的部分作为耕地，要使得耕地的面积为504m2，道路的宽应为多少？