题目内容
12．
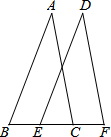已知：如图，∠B=∠DEF，∠ACB=∠F，BE=CF．求证：AB=DE．
分析 证明它们所在的三角形全等即可．根据∠B=∠DEF，∠ACB=∠F；由BE=CF可得BC=EF．运用ASA证明△ABC与△DEF全等，再根据全等三角形的性质解答即可．
解答 解：∵BE=CF，
∴BC=EF．
在△ABC与△DEF中，
$\left\{\begin{array}{l}{∠B=∠DEF}\\{BC=EF}\\{∠ACB=∠F}\end{array}\right.$，
∴△ABC≌△DEF（ASA），
∴AB=DE．
点评 此题考查全等三角形的判定与性质，属基础题．证明线段相等，通常证明它们所在的三角形全等．
练习册系列答案
阅读快车系列答案
相关题目
7．
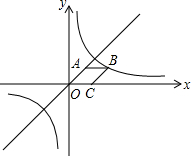如图，点C在x轴的正半轴上，菱形OCBA的面积为$\sqrt{2}$，点B在双曲线y=$\frac{k}{x}$上，点A在直线y=x上，则k的值为（ ）
如图，点C在x轴的正半轴上，菱形OCBA的面积为$\sqrt{2}$，点B在双曲线y=$\frac{k}{x}$上，点A在直线y=x上，则k的值为（ ）| A． | 1+$\frac{{\sqrt{2}}}{2}$ | B． | 1+$\sqrt{2}$ | C． | $\sqrt{2}$+2 | D． | 2$\sqrt{2}$ |
试判断如图所示的两个矩形是否相似．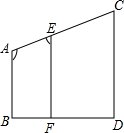
填写完整过程：