题目内容
1.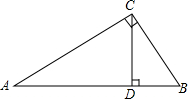 如图,Rt△ABC中,CD是斜边AB上的高.求证:
如图,Rt△ABC中,CD是斜边AB上的高.求证:(1)△ACD∽△ABC;
(2)△CBD∽△ABC.
分析 (1)根据有两组角对应相等的两个三角形相似进行证明即可.
(2)根据有两组角对应相等的两个三角形相似进行证明即可.
解答 证明:(1)∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵∠A=∠A,
∴△ACD∽△ABC.
(2)∵CD是斜边AB上的高,
∴∠BDC=90°,
∴∠BDC=∠ACB,
∵∠B=∠B,
∴△CBD∽△ABC.
点评 本题考查了相似三角形的判定定理;熟记有两组角对应相等的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
11.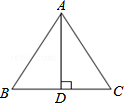 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )| A. | BD=CD | B. | ∠DAB=∠DAC | ||
| C. | 当∠B=60°时,AB=2BD | D. | 高AD是△ABC的对称轴 |
9.若a,b,c是△ABC的三边长,则a2-2ab-c2+b2的值( )
| A. | 大于零 | B. | 小于零 | ||
| C. | 等于零 | D. | 与零的大小没有关系 |
10. 如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
 如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )| A. | 3m | B. | 2m | C. | 4m | D. | $\sqrt{3}$m |