题目内容
20.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$不平行,$\overrightarrow{c}=\overrightarrow{a}+2\overrightarrow{b}$,实数x、y满足$2x\overrightarrow{a}+(5-y)\overrightarrow{b}=(3y+2)\overrightarrow{a}+3x\overrightarrow{c}$,求x、y的值.分析 由平面向量$\overrightarrow{a}$、$\overrightarrow{b}$不平行,$\overrightarrow{c}=\overrightarrow{a}+2\overrightarrow{b}$,实数x、y满足$2x\overrightarrow{a}+(5-y)\overrightarrow{b}=(3y+2)\overrightarrow{a}+3x\overrightarrow{c}$,可得2x$\overrightarrow{a}$+(5-y)$\overrightarrow{b}$=(3x+3y+2)$\overrightarrow{a}$+6x$\overrightarrow{b}$,继而可得方程组:$\left\{\begin{array}{l}{2x=3x+3y+2}\\{5-y=6x}\end{array}\right.$,解此方程组即可求得答案.
解答 解:∵平面向量$\overrightarrow{a}$、$\overrightarrow{b}$不平行,$\overrightarrow{c}=\overrightarrow{a}+2\overrightarrow{b}$,$2x\overrightarrow{a}+(5-y)\overrightarrow{b}=(3y+2)\overrightarrow{a}+3x\overrightarrow{c}$,
∴2x$\overrightarrow{a}$+(5-y)$\overrightarrow{b}$=(3y+2)$\overrightarrow{a}$+3x($\overrightarrow{a}$+2$\overrightarrow{b}$),
∴2x$\overrightarrow{a}$+(5-y)$\overrightarrow{b}$=(3x+3y+2)$\overrightarrow{a}$+6x$\overrightarrow{b}$,
∴$\left\{\begin{array}{l}{2x=3x+3y+2}\\{5-y=6x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$,
∴x=1,y=-1.
点评 此题考查了平面向量的知识.注意根据题意构造方程组$\left\{\begin{array}{l}{2x=3x+3y+2}\\{5-y=6x}\end{array}\right.$是解此题的关键.

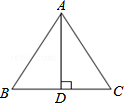 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )| A. | BD=CD | B. | ∠DAB=∠DAC | ||
| C. | 当∠B=60°时,AB=2BD | D. | 高AD是△ABC的对称轴 |
| A. | 大于零 | B. | 小于零 | ||
| C. | 等于零 | D. | 与零的大小没有关系 |
 如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )| A. | 3m | B. | 2m | C. | 4m | D. | $\sqrt{3}$m |
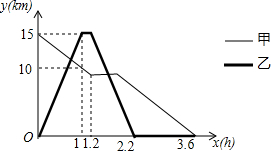 某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.