题目内容
19.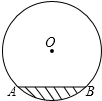 如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少?
如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少?
分析 过O作OC垂直于AB,利用垂径定理得到C为AB的中点,在直角三角形AOC中,由水面高度与半径求出OC的长,利用勾股定理求出AC的长,即可确定出AB的长.
解答  解:过O作OC⊥AB,交AB于点C,可得出AC=BC=$\frac{1}{2}$AB,
解:过O作OC⊥AB,交AB于点C,可得出AC=BC=$\frac{1}{2}$AB,
由水面高为6,半径为12,得到OC=6,
在Rt△AOC中,根据勾股定理得:AC=$\sqrt{O{A}^{2}-O{C}^{2}}=\sqrt{1{2}^{2}-{6}^{2}}=6\sqrt{3}$,
则AB=2AC=12$\sqrt{3}$.
点评 此题考查了垂径定理的应用,以及勾股定理,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
4.小明家电冰箱冷藏室的温度是6℃,冷冻室的温度比冷藏室的温度低24℃,那么这台电冰箱冷冻室的温度为( )
| A. | 30℃ | B. | -16℃ | C. | -22℃ | D. | -18℃ |
11.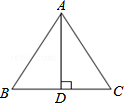 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )| A. | BD=CD | B. | ∠DAB=∠DAC | ||
| C. | 当∠B=60°时,AB=2BD | D. | 高AD是△ABC的对称轴 |
9.若a,b,c是△ABC的三边长,则a2-2ab-c2+b2的值( )
| A. | 大于零 | B. | 小于零 | ||
| C. | 等于零 | D. | 与零的大小没有关系 |
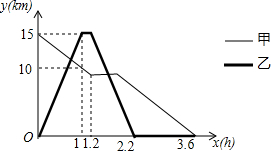 某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.