题目内容
9.在数学兴趣小组活动中,小明进行数学探究活动,将边长为$\sqrt{2}$的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.

分析 (1)根据正方形的性质得出AD=AB,AG=AE,∠DAG=∠BAE=90°,再利用SAS证明△DAG≌△BAE,根据全等三角形对应边相等即可得出DG=BE;
(2)分两种情况:①C在EA的延长线上,连结BD交AC于O,求出OB、OE,然后在Rt△BOE中利用勾股定理可求出BE的长;②C在AE上,证明C与E重合,那么BE=BC=$\sqrt{2}$.
解答  解:(1)如图1,∵四边形ABCD与四边形AEFG都是正方形,
解:(1)如图1,∵四边形ABCD与四边形AEFG都是正方形,
∴AD=AB,AG=AE,∠DAG=∠BAE=90°.
在△DAG与△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAG=∠BAE}\\{AG=AE}\end{array}\right.$,
∴△DAG≌△BAE,
∴DG=BE;
(2)将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,分两种情况:
①如果C在EA的延长线上时,
如备用图1,连结BD交AC于O,
∵正方形ABCD边长为$\sqrt{2}$,
∴BD=AC=$\sqrt{2}$AB=2,AC⊥BD,
∴OB=OA=$\frac{1}{2}$BD=1. ∵正方形AEFG边长为2,
∵正方形AEFG边长为2,
∴OE=OA+AE=1+2=3.
在Rt△BOE中,∵∠BOE=90°,
∴BE=$\sqrt{O{B}^{2}+O{E}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
②如果C在AE上时,
如备用图2,连结BD交AC于O,
∵正方形ABCD边长为$\sqrt{2}$,
∴BC=AC=$\sqrt{2}$AB=2,
∵正方形AEFG边长为2,
∴AE=2,
∴C与E重合,
∴BE=BC=$\sqrt{2}$.
故所求BE的长为$\sqrt{10}$或$\sqrt{2}$.
点评 本题是四边形综合题,考查了正方形的性质,全等三角形的判定与性质,旋转的性质,勾股定理,难度适中.利用分类讨论、数形结合是解题的关键.

| A. | $\frac{400}{x}=\frac{300}{x-30}$ | B. | $\frac{400}{x-30}=\frac{300}{x}$ | C. | $\frac{400}{x+30}=\frac{300}{x}$ | D. | $\frac{400}{x}=\frac{300}{x+30}$ |
| A. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | B. | (x+$\frac{1}{4}$)2=$\frac{9}{16}$ | C. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | D. | (x+$\frac{1}{2}$)2=$\frac{5}{4}$ |
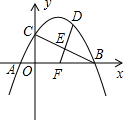 如图,二次函数y=ax2+$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(-1,0),点C(0,2).
如图,二次函数y=ax2+$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(-1,0),点C(0,2).



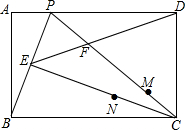 如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.
如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.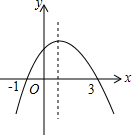 如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法:
如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法: