题目内容
4.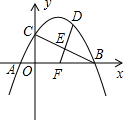 如图,二次函数y=ax2+$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(-1,0),点C(0,2).
如图,二次函数y=ax2+$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(-1,0),点C(0,2).(1)求抛物线的函数解析式,并求出该抛物线的顶点坐标;
(2)若点D是抛物线在第一象限的部分上的一动点,
①当四边形OCDB的面积最大时,求点D的坐标;
②若E为BC的中点,DE的延长线交线段AB于点F,当△BEF为钝角三角形时,请直接写出点D的纵坐标y的范围.
分析 (1)把A点和B点B坐标代入y=ax2+$\frac{3}{2}$x+c得到a、c的方程组,然后解方程组求出a、c即可得到抛物线的解析式,然后把一般式配成顶点式即可得到顶点坐标;
(2)①先解方程-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0得B(4,0),设D(t,-$\frac{1}{2}$t2+$\frac{3}{2}$t+2),根据三角形面积公式,利用S四边形OCDB=S△OCD+S△ODB得到四边形OCDB的面积=-t2+4t+4,然后根据二次函数的性质求解;
②先利用线段中点坐标公式得到E(2,1),然后分类:分别求出∠EFB=90°和∠BEF=90°时D点坐标,再求出直线AE与抛物线的交点,则可得到点D的纵坐标y的范围.
解答 解:(1)把A(-1,0),C(0,2)代入y=ax2+$\frac{3}{2}$x+c得$\left\{\begin{array}{l}{a-\frac{3}{2}+c=0}\\{c=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$,
所以抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,
因为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$,
所以抛物线的顶点坐标为($\frac{3}{2}$,$\frac{25}{8}$);
(2)①当x=0时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,解得x1=-1,x2=4,则B(4,0),
设D(t,-$\frac{1}{2}$t2+$\frac{3}{2}$t+2),
S四边形OCDB=S△OCD+S△ODB=$\frac{1}{2}$•2•t+$\frac{1}{2}$•4•(-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)=-t2+4t+4=-(t-2)2+8,
所以当t=2时,四边形OCDB的面积最大,此时D点坐标为(2,3);
②∵E为BC的中点,
∴E(2,1),
若DF⊥AB时,∠EFB=90°,此时D(2,3),当0<x<2时,∠EFB为钝角,此时点D的纵坐标y的范围为2<y≤$\frac{25}{8}$,
若FD⊥BC,∠BEF=90°,BE=$\sqrt{(4-2)^{2}+{1}^{2}}$=$\sqrt{5}$,BC=2$\sqrt{5}$,
∵∠EBF=∠OBC,
∴Rt△BEF∽Rt△BOC,
∴BF:BC=BE:BO,即BF:2$\sqrt{5}$=$\sqrt{5}$:4,解得BF=$\frac{5}{2}$,
∴OF=OB-BF=$\frac{3}{2}$,
∴F($\frac{3}{2}$,0),
易得直线此时EF的解析式为y=2x-3,
解方程组$\left\{\begin{array}{l}{y=2x-3}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{41}}{2}}\\{y=\sqrt{41}-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{41}}{2}}\\{y=-\sqrt{41}-4}\end{array}\right.$,则D($\frac{-1+\sqrt{41}}{2}$,$\sqrt{41}$-4),
设直线AE的解析式为uy=kx+b,
把A(-1,0),E(2,1)代入得$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$,
∴直线AE的解析式为y=$\frac{1}{3}$x+$\frac{1}{3}$,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{1}{3}}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{13}{9}}\end{array}\right.$,
∴当$\frac{-1+\sqrt{41}}{2}$<x≤$\frac{10}{3}$时,∠BEF为钝角,此时点D的纵坐标y的范围为$\frac{13}{9}$≤y<$\sqrt{41}$-4,
综上所述,点D纵坐标y的取值范围为$\frac{13}{9}≤y≤\frac{25}{8}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;理解坐标与图形的性质,记住两点间的距离公式;会利用相似三角形的知识求线段的长;能运用分类讨论的思想解决数学问题.

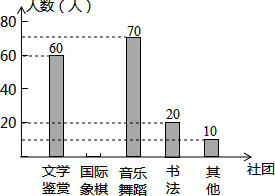 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
| 所占百分比 | a | 20% | b | 10% | 5% |
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
| A. | x≠1 | B. | x≠3 | C. | x≥1且x≠3 | D. | x≥3且x≠1 |
| A. | 3 | B. | -3 | C. | 2a-3 | D. | 2a+3 |
| A. |  | B. |  | C. |  | D. |  |

 在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )
在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )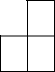


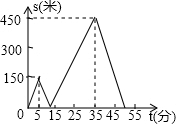 甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法
甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法 若抛物线y=ax2+bx+c如图所示,下列四个结论:
若抛物线y=ax2+bx+c如图所示,下列四个结论: