题目内容
1.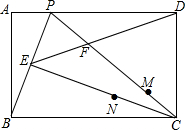 如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.
如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求$\frac{PF}{PC}$的值(用含k的代数式表示);
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k=$\sqrt{2}$时,求NF+NM的最小值.
分析 (1)根据矩形的想知道的∠A=∠ABC=90°,由余角的性质得到∠APB=∠PBC,根据相似三角形的判定定理即可得到结论;
(2)①根据相似三角形的性质得到$\frac{AP}{AB}=\frac{BE}{BC}$,得到BP=$\sqrt{9+{k}^{2}}$,过P作PH⊥PD交DE于H,推出P,E.C,D四点共圆,根据圆周角定理得到∠PDH=∠PCE=∠BCE=∠ABP,根据相似三角形的想知道的$\frac{PH}{PD}=\frac{AP}{AB}$,即可得到结论;②把k=$\sqrt{2}$代入$\frac{PF}{FC}=\frac{9-2}{18}$=$\frac{7}{18}$,过F作FG⊥BC于G交CE于N,反向延长交AD于H,则FH⊥AD,过N作NM⊥PC于M,根据线段公理得到NF+NM的最小值即为FG的长,即可得到结论.
解答  (1)证明:在矩形ABCD中,
(1)证明:在矩形ABCD中,
∵∠A=∠ABC=90°,
∵CE⊥BP,
∴∠CEB=90°,
∴∠A=∠CEB,
∴∠APB+∠ABP=∠ABP+∠PBC=90°,
∴∠APB=∠PBC,
∴△ABP∽△ECB;
(2)解:①∵△ABP∽△ECB,
∴$\frac{AP}{BP}=\frac{BE}{BC}$,
∵BP=$\sqrt{9+{k}^{2}}$,E为BP的中点,
∴BE=$\frac{\sqrt{9+{k}^{2}}}{2}$,
∴BC=$\frac{9+{k}^{2}}{2k}$,
过P作PH⊥PD交DE于H,
∴PD=BC-AP=$\frac{9-{k}^{2}}{2k}$,
∵∠BEC=∠ADC=90°,
∴P,E.C,D四点共圆,
∴∠PDH=∠PCE=∠BCE=∠ABP,
∴△APB∽△PHD,
∴$\frac{PH}{PD}=\frac{AP}{AB}$,
∴PH=$\frac{9-{k}^{2}}{6}$,
∴$\frac{PF}{PC}$=$\frac{PF}{FC+PF}=\frac{9-{k}^{2}}{27-{k}^{2}}$;
②当k=$\sqrt{2}$时,$\frac{PF}{FC}=\frac{7}{25}$,
过F作FG⊥BC于G交CE于N,反向延长交AD于H,
则FH⊥AD,过N作NM⊥PC于M,
∴NF+NM的最小值即为FG的长,
∴$\frac{FG}{FH}$=$\frac{FC}{PF}$=$\frac{25}{7}$,
∴FG=$\frac{54}{25}$,
即NF+NM的最小值是$\frac{54}{25}$.
点评 本题考查了相似三角形的判定和性质,四点共圆,勾股定理,最短距离问题,正确的作出辅助线构造相似三角形是解题的关键,

 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )| A. | $\frac{{2}^{2n}-2}{{2}^{2n}}$ | B. | $\frac{{2}^{n}-1}{{2}^{2n-1}}$ | C. | $\frac{{3}^{n}-1}{{2}^{2n}}$ | D. | $\frac{{2}^{n-1}-1}{{2}^{2n}}$ |
| A. | 3 | B. | -3 | C. | 2a-3 | D. | 2a+3 |
 如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )
如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )| A. | 12π-$\frac{9\sqrt{3}}{2}$ | B. | 4π-$\frac{9\sqrt{3}}{2}$ | C. | 12π-9$\sqrt{3}$ | D. | 4π-9$\sqrt{3}$ |

 在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )
在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )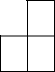


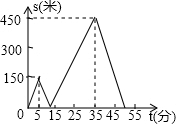 甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法
甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法