题目内容
7.(1)计算:2(sin60°+cos45°)+(2-tan45°)-cot30°.(2)$\frac{{{x^2}+1}}{{{x^2}-1}}-\frac{{3{x^2}-3}}{{{x^2}+1}}-2=0$.
分析 (1)原式利用特殊角的三角函数值计算即可得到结果;
(2)设y=$\frac{{x}^{2}+1}{{x}^{2}-1}$,方程变形后,求出解得到y的值,即可确定出x的值.
解答 解:(1)原式=2($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$)+(2-1)-$\sqrt{3}$=$\sqrt{3}$+$\sqrt{2}$+1-$\sqrt{3}$=$\sqrt{2}$+1;
(2)设y=$\frac{{x}^{2}+1}{{x}^{2}-1}$,
方程整理得:y-$\frac{3}{y}$-2=0,
去分母得:y2-2y-3=0,即(y-3)(y+1)=0,
解得:y=3或y=-1,
经检验y=3与y=-1都为分式方程的解,
当y=3时,$\frac{{x}^{2}+1}{{x}^{2}-1}$=3,解得:x=±$\sqrt{2}$;当y=-1时,$\frac{{x}^{2}+1}{{x}^{2}-1}$=-1,解得:x=±$\sqrt{2}$,
经检验x=±$\sqrt{2}$都为原方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
18.用公式解方程-3x2+5x-1=0,正确的是( )
| A. | x=$\frac{-5±\sqrt{13}}{6}$ | B. | x=$\frac{-5±\sqrt{13}}{3}$ | C. | x=$\frac{5±\sqrt{13}}{6}$ | D. | x=$\frac{5±\sqrt{13}}{3}$ |
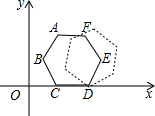 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(50,2)的是点A.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(50,2)的是点A.