题目内容
在平面直角坐标系中,已知点P(1-2m,
)关于y轴的对称点Q在第四象限,且m为整数.
(1)求整数m的值;
(2)求△OPQ的面积.
| 3m-4 |
| 3 |
(1)求整数m的值;
(2)求△OPQ的面积.
考点:关于x轴、y轴对称的点的坐标,解一元一次不等式组
专题:
分析:(1)首先根据关于y轴对称点的坐标特点可得点Q坐标为(-1+2m,
),再根据第四象限内点的坐标特点可得
,再解不等式可得m的取值范围,进而得到m的值;
(2)由m的值可得Q、P点坐标,进而得到QP的长,再利用三角形的面积公式计算出面积即可.
| 3m-4 |
| 3 |
|
(2)由m的值可得Q、P点坐标,进而得到QP的长,再利用三角形的面积公式计算出面积即可.
解答:解:(1)点点P(1-2m,
)关于y轴的对称点Q坐标为(-1+2m,
),
∵Q在第四象限,
∴
,解得
<m<
;
∵m为整数,
∴m=1;
(2)∵m=1,
∴P(-1,-
),Q(1,-
;
∴PQ=2,
∴S△OPQ=
×2×
=
.
| 3m-4 |
| 3 |
| 3m-4 |
| 3 |
∵Q在第四象限,
∴
|
| 1 |
| 2 |
| 4 |
| 3 |
∵m为整数,
∴m=1;
(2)∵m=1,
∴P(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
∴PQ=2,
∴S△OPQ=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了关于y轴对称点的坐标特点,以及一元一次不等式组的解法,关键是正确确定m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 将连续正整数按图所示的规律排列,观察图表并回答下列问题:
将连续正整数按图所示的规律排列,观察图表并回答下列问题: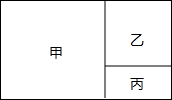 如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?
如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?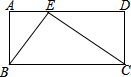 如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE:ED=9:16.
如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE:ED=9:16.