题目内容
 将连续正整数按图所示的规律排列,观察图表并回答下列问题:
将连续正整数按图所示的规律排列,观察图表并回答下列问题:(1)在第1列第2013行的数是
(2)在第1行第n列的数是
(3)位于第7行第7列的数是多少?为什么?
考点:规律型:数字的变化类
专题:
分析:(1)由第一列的数可知:1=1,2=1+1,4=1+1+2,7=1+1+2+3,…得出第1列第n行的数为1+1+2+3+…+(n-1)=
+1;由此代入2013得出答案即可;
(2)由第一行的数可知:1=1,3=1+2,6=1+2+3,10=1+2+3+4,…得出在第1行第n列的数是1+2+3+4+…+n=
;
(3)由第1行第1列数是1,第2行第2列数是1+4,第3行第3列数是1+4+8,…第n行第n列数是1+4+8+…+4(n-1)=1+4(1+2+3+…+(n-1))=1+2n(n-1);由此代入求得答案即可.
| n(n-1) |
| 2 |
(2)由第一行的数可知:1=1,3=1+2,6=1+2+3,10=1+2+3+4,…得出在第1行第n列的数是1+2+3+4+…+n=
| n(n+1) |
| 2 |
(3)由第1行第1列数是1,第2行第2列数是1+4,第3行第3列数是1+4+8,…第n行第n列数是1+4+8+…+4(n-1)=1+4(1+2+3+…+(n-1))=1+2n(n-1);由此代入求得答案即可.
解答:解:(1)∵1=1,
2=1+1,
4=1+1+2,
7=1+1+2+3,
…
∴第1列第n行的数为1+1+2+3+…+(n-1)=
+1,
当n=2013时,原式=2025079;
(2)∵1=1,
3=1+2,
6=1+2+3,
10=1+2+3+4,
…
∴第1行第n列的数是1+2+3+4+…+n=
;
(3)∵1=1,
5=1+4,
13=1+4+8,
25=1+4+8+12,
…
∴第n行第n列的数是1+4+8+12+…+4(n-1)=1+4(1+2+3+…+(n-1))=1+2n(n-1);
∴第七行第七列的数是 1+2×7×(7-1)=85.
2=1+1,
4=1+1+2,
7=1+1+2+3,
…
∴第1列第n行的数为1+1+2+3+…+(n-1)=
| n(n-1) |
| 2 |
当n=2013时,原式=2025079;
(2)∵1=1,
3=1+2,
6=1+2+3,
10=1+2+3+4,
…
∴第1行第n列的数是1+2+3+4+…+n=
| n(n+1) |
| 2 |
(3)∵1=1,
5=1+4,
13=1+4+8,
25=1+4+8+12,
…
∴第n行第n列的数是1+4+8+12+…+4(n-1)=1+4(1+2+3+…+(n-1))=1+2n(n-1);
∴第七行第七列的数是 1+2×7×(7-1)=85.
点评:此题考查数字的变化规律,找出数字之间的联系,得出规律,利用规律解决问题.

练习册系列答案
相关题目
 AB为⊙O的直径,弦CD⊥AB,垂足为E,下列结论中错误的是( )
AB为⊙O的直径,弦CD⊥AB,垂足为E,下列结论中错误的是( )| A、CE=DE | ||||
B、
| ||||
| C、∠BAC=∠BAD | ||||
| D、AC=ED |

 小明从A地出发,水平向右走100m后向左转20°,再沿直线前进100m,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走了
小明从A地出发,水平向右走100m后向左转20°,再沿直线前进100m,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走了 如图,一根钢管放在V形架内,其横截面如图所示,钢管的半径是25cm.
如图,一根钢管放在V形架内,其横截面如图所示,钢管的半径是25cm.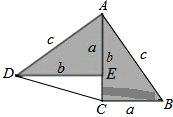 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.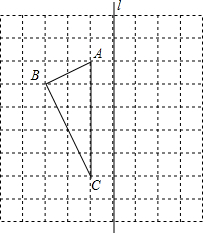 如图,正方形网格中每个小正方形边长都是1.
如图,正方形网格中每个小正方形边长都是1.