题目内容
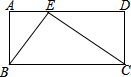 如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE:ED=9:16.
如图,在长方形ABCD中,AB=24,AD=50,E是AD上一点,且AE:ED=9:16.(1)求BE、CE的长;
(2)△BEC是否为直角三角形?为什么?
考点:勾股定理,勾股定理的逆定理
专题:
分析:(1)根据已知条件易求AE,DE的长,再由勾股定理即可求出BE,CE的长;
(2)△BEC是直角三角形.根据勾股定理的逆定理判定即可.
(2)△BEC是直角三角形.根据勾股定理的逆定理判定即可.
解答:解:(1)∵AD=50,E是AD上一点,且AE:ED=9:16,
∴AE=18,DE=32,
∵AB=24,
∴BE=
=30,CE=
=40;
(2)△BEC是直角三角形.理由如下:
∵BE=30,CE=40,BC=50,
∴BE2+CE2=BC2,
∴△BEC是直角三角形.
∴AE=18,DE=32,
∵AB=24,
∴BE=
| AE2+AB2 |
| DE2+CD2 |
(2)△BEC是直角三角形.理由如下:
∵BE=30,CE=40,BC=50,
∴BE2+CE2=BC2,
∴△BEC是直角三角形.
点评:本题考查了勾股定理以及逆定理的运用,解题的关键是熟记其定理和逆定理以及矩形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列长度的四组线段中,不可以构成直角三角形的是( )
A、1,2,
| ||
| B、12,5,13 | ||
| C、3,4,5 | ||
| D、8,15,18 |
在代数式
中,x的取值范围在数轴上可表示为( )
| x-1 |
A、 |
B、 |
C、 |
D、 |
若分式
不论x取何实数总有意义,则m的取值范围是( )
| 1 |
| x2-9x+m |
| A、m≥9 | B、m≤9 |
| C、m>9 | D、m<9 |
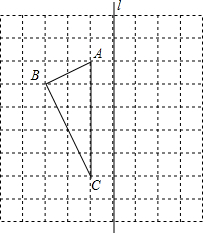 如图,正方形网格中每个小正方形边长都是1.
如图,正方形网格中每个小正方形边长都是1.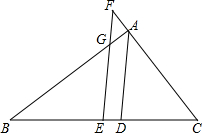 如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF与于点G.若BG=CF,求证:AD为△ABC的角平分线.
如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF与于点G.若BG=CF,求证:AD为△ABC的角平分线.