题目内容
18.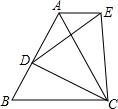 如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
分析 (1)根据等边三角形的边相等和角为60°得:BC=AC,DC=CE,∠ACB=∠DCE=60°,所以∠BCD=∠ACE,根据SAS可证明△ACE≌△BCD;
(2)证明∠CAE=∠ACB,得AE∥BC.
解答 证明:(1)∵△ABC和△DCE都是等边三角形,
∴BC=AC,DC=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCA=∠DCE-∠DCA,
即∠BCD=∠ACE,
在△ACE和△BCD中,
∵$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=CE}\end{array}\right.$,
∴△ACE≌△BCD(SAS);
(2)AE∥BC,理由是:
∵△ACE≌△BCD,
∴∠CAE=∠ABC,
∵△ABC是等边三角形,
∴∠ABC=∠ACB,
∴∠CAE=∠ACB,
∴AE∥BC.
点评 本题考查了三角形全等的性质和判定、等边三角形的性质;熟练掌握全等三角形的判定方法:SAS、AAS、ASA、SSS,对于两边的位置关系:平行或垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.圆上有两点A,B,劣弧AB的度数为120°,那么,优弧AB所对的圆心角的度数为( )
| A. | 80° | B. | 120° | C. | 180° | D. | 240° |
13.张老师周末到某家居建材市场购买沙发、橱窗和地板三样物品,碰巧该市场推出“迎圣诞元旦双节”优惠活动,具体优惠情况如下:
(1)若购买三样物品原价8000元,请求出张老师实际的付款金额?
(2)若购买三样物品实际花费了6820元.
①请求出三件物品的原价总共是多少钱?
②几天后,张老师发现地板的样式不适合需要退货,该市场规定:消费者需支付优惠差额(即退货商品在购买时所享受的优惠),并且还要支付商品原价5%的手续费,最终该市场退还了张老师2345元,请问地板原价是多少钱?
| 购物总金额(原价) | 优惠率 |
| 不超过5000元的部分 | 10% |
| 超过5000元且不超过10000元的部分 | 20% |
| 超过10000元且不超过20000元的部分 | 30% |
| … | … |
(2)若购买三样物品实际花费了6820元.
①请求出三件物品的原价总共是多少钱?
②几天后,张老师发现地板的样式不适合需要退货,该市场规定:消费者需支付优惠差额(即退货商品在购买时所享受的优惠),并且还要支付商品原价5%的手续费,最终该市场退还了张老师2345元,请问地板原价是多少钱?
10.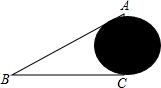 如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
 如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )
如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130m,BC=120m,若每天凿隧道5m,则把隧道凿通需要( )| A. | 10天 | B. | 9天 | C. | 8天 | D. | 11天 |
8.下列实数中,有理数是( )
| A. | $\sqrt{8}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101 001 001 |
 方格中,除9和-2外其余字母各表示一个数,已知方格中任意三个连续方格中的数之和为19,求A+H+M+N的值.
方格中,除9和-2外其余字母各表示一个数,已知方格中任意三个连续方格中的数之和为19,求A+H+M+N的值.