题目内容
6.若实数x,y满足$\sqrt{2x-1}+2(y-1)^{2}=0$,则x+y的值等于$\frac{3}{2}$.分析 直接利用偶次方的性质以及二次根式的性质得出x,y的值进而得出答案.
解答 解:∵$\sqrt{2x-1}+2(y-1)^{2}=0$,
∴2x-1=0,y-1=0,
解得:x=$\frac{1}{2}$,y=1,
则x+y=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题主要考查了偶次方的性质以及二次根式的性质,正确掌握相关性质是解题关键.

练习册系列答案
相关题目
17.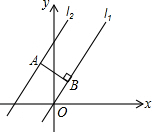 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{12}{5}$ |
11.在Rt△ABC中,如果∠C=90°,AB=10,BC=8,那么cosB的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |

 如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.
如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.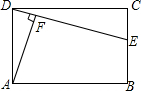 如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.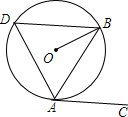 如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.
如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.