Question

17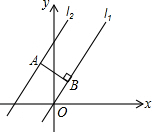．如图，在平面直角坐标系中，已知l₁∥l₂，直线l₁经过原点O，直线l₂对应的函数表达式为$y=\frac{4}{3}x+4$，点A在直线l₂上，AB⊥l₁，垂足为B，则线段AB的长为（　　）

• A． 2
• B． 3
• C． 4
• D． $\frac{12}{5}$

Answer 1

分析 过点O作OC垂直于l₂交点为C，得出四边形OCAB是矩形，则OC=AB；分别求得l₂与两个坐标轴的交点坐标，在l₂与两个坐标轴围成的直角三角形中利用勾股定理与三角形的面积求得OC即可得出答案．

解答 解：如图，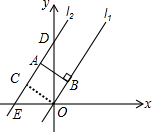

过点O作OC垂直于l₂交点为C，
∵l₁∥l₂，AB⊥l₁，OC⊥l₂，
∴四边形OCAB是矩形，
∴OC=AB；
∵直线l₂与两个坐标轴的交点坐标分别为D（0，4），E（-3，0），
∴DE=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴$\frac{1}{2}$DE•OC=$\frac{1}{2}$OE•OD，
即$\frac{1}{2}$×5×OC=$\frac{1}{2}$×3×4，
解得：OC=$\frac{12}{5}$．
∴AB=$\frac{12}{5}$．
故选：D．

点评 本题考查了两直线相交或平行问题，若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同；以及勾股定理，矩形的判定等知识的综合运用．