Question

18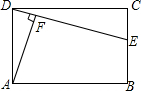．如图所示，在矩形ABCD中，E是BC上一点，AF⊥DE于点F．
（1）求证：DF•CD=AF•CE．
（2）若AF=4DF，CD=12，求CE的长．

Answer 1

分析 （1）根据四边形ABCD是矩形可得出∠ADC=∠C=90°，再根据相似三角形的判定定理可得出△ADF∽△DCE，由相似三角形的对应边成比例即可得出结论；
（2）由（1）可知DF：AF=CE：DC，再结合已知条件即可求出CE的长．

解答 （1）证明：
∵四边形ABCD是矩形，
∴∠ADC=∠C=90°，
∴∠ADF+∠CDE=90°，
∵AF⊥DE，
∴∠AFD=∠DAF+∠FDA=90°，
∴∠FAD=∠CDE，
又∵∠C=∠AFD=90°，
∴△ADF∽△DCE；
∴$\frac{DF}{CE}=\frac{AF}{DC}$，
即DF•CD=AF•CE；
（2）∵△ADF∽△DCE；
∴$\frac{DF}{CE}=\frac{AF}{DC}$，
∴$\frac{DF}{AF}=\frac{CE}{DC}$，
又∵AF=4DF，CD=12，
∴$\frac{DF}{4DF}=\frac{CE}{12}$，
∴CE=3．

点评 本题考查的是相似三角形的判定与性质以及垂直的性质和矩形的性质运用，能根据题意得出△ADF∽△DCE是解答此题的关键．