题目内容
16.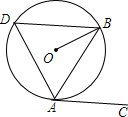 如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.
如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.(1)求∠OBA的度数;
(2)求∠D的度数.
分析 (1)连接OA,由切线的性质可得∠OAC=90°,再由已知条件可求出∠OAB的度数,由圆的性质可得△OAB是等腰三角形,根据等边对等角即可求出∠OBA的度数;
(2)由(1)可知△OAB是等腰三角形,所以∠AOB的度数可求,再由圆周角定理即可求出∠D度数.
解答 解:(1)连接OA,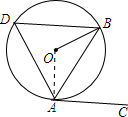
∵AC与⊙O相切于点A,
∴OA⊥AC,
∴∠OAC=90°,
∵∠BAC=52°,
∴∠OAB=38°,
∵OA=OB,
∴∠OBA=∠OAB=38°;
(2)∵∠OBA=∠OAB=38°,
∴∠AOB=180°-2×38°=104°,
∴∠D=$\frac{1}{2}$∠AOB=52°.
点评 此题考查了切线的性质,圆周角定理以及等腰三角形的判定和性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 互为相反数的两个数的绝对值相等 | |
| B. | 最小的整数是0 | |
| C. | 有理数分为正数和负数 | |
| D. | 如果两个数的绝对值相等,那么这两个数相等 |
8.二次函数y=(x-3)2+2的顶点坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (3,-2) | D. | (-3,1) |
5.已知y=(m-2)x|m|+2是y关于x的二次函数,那么m的值为( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 0 |
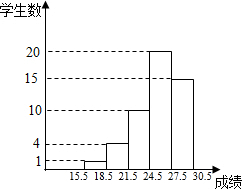 依据某校九(1)班在体育毕业考试中全班所有学生成绩,制成的频数分布直方图如图(学生成绩取整数),则成绩在21.5-24.5这一分数段的频数是( )
依据某校九(1)班在体育毕业考试中全班所有学生成绩,制成的频数分布直方图如图(学生成绩取整数),则成绩在21.5-24.5这一分数段的频数是( )