题目内容
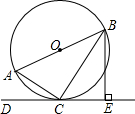 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠A=60°,求CE的长.
考点:切线的判定
专题:
分析:(1)如图,作辅助线;证明∠OCB=∠CBE,得到OC∥BE;由BE⊥DE,得到OC⊥DE,即可解决问题.
(2)求出AC=2,BC=2
;证明∠ACB=∠BEC,∠ABC=∠CBE,得到△ABC∽△CBE,进而得到
=
,求出CE=
.
(2)求出AC=2,BC=2
| 3 |
| AB |
| BC |
| AC |
| CE |
| 3 |
解答: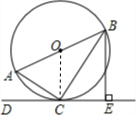 解:(1)如图,连接OC;
解:(1)如图,连接OC;
∵BC平分∠ABE,OB=OC,
∴∠OBC=∠OCB,∠OBC=∠CBE,
∴∠OCB=∠CBE,
∴OC∥BE;而BE⊥DE,
∴OC⊥DE,
即DE是⊙O的切线.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,而∠A=60°,
∴∠ABC=30°,AC=
AB=2,
BC=
×4=2
;
∵∠ACB=∠BEC,∠ABC=∠CBE,
∴△ABC∽△CBE,
∴
=
,CE=
.
 解:(1)如图,连接OC;
解:(1)如图,连接OC;∵BC平分∠ABE,OB=OC,
∴∠OBC=∠OCB,∠OBC=∠CBE,
∴∠OCB=∠CBE,
∴OC∥BE;而BE⊥DE,
∴OC⊥DE,
即DE是⊙O的切线.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,而∠A=60°,
∴∠ABC=30°,AC=
| 1 |
| 2 |
BC=
| ||
| 2 |
| 3 |
∵∠ACB=∠BEC,∠ABC=∠CBE,
∴△ABC∽△CBE,
∴
| AB |
| BC |
| AC |
| CE |
| 3 |
点评:该题主要考查了圆的切线的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用切线的判定及其质、相似三角形的判定及其性质等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
下列是方程5x2-x=6的解的是( )
| A、x=1 | B、x=-1 |
| C、x=-2 | D、x=2 |
 如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.
如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.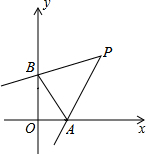 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
 如图,将右边的图案变成左边的图案,是通过
如图,将右边的图案变成左边的图案,是通过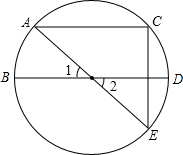 如图,直径AE,BD交于点O,点D为
如图,直径AE,BD交于点O,点D为
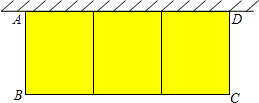 如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.