题目内容
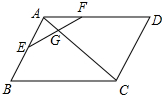如图，在平行四边形ABCD中，E、F分别在AB、AD上，EF交AC于点G，若AE：EB=2：3，AF：FD=3：2，则AG：AC等于多少？考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：如图，作辅助线；证明△AEH∽△ABC，得到
=
=
①；证明△AFG∽△HEG，得到
=
；证明AG=
AH，求出
=
×
=
．
| AH |
| AC |
| EH |
| BC |
| 2 |
| 5 |
| AG |
| GH |
| AF |
| EH |
| 3 |
| 5 |
| AG |
| AC |
| 3 |
| 5 |
| AH |
| AC |
| 6 |
| 25 |
解答：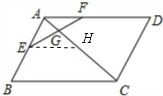
解：如图，过点E作EH∥BC；
∴△AEH∽△ABC，
∴
=
=
，而
=
，
∴
=
=
①；
∵四边形ABCD为平行四边形，
∴BC=AD；AD∥BC，
∴AF∥EH，△AFG∽△HEG，
∴
=
；
设AF=3λ，则DF=2λ，
∴BC=AD=5λ，代入①式得EH=2λ；
∴
=
，AG=
AH，
∴
=
×
=
．
解：如图，过点E作EH∥BC；∴△AEH∽△ABC，
∴
| AH |
| AC |
| EH |
| BC |
| AE |
| AB |
| AE |
| EB |
| 2 |
| 3 |
∴
| AH |
| AC |
| EH |
| BC |
| 2 |
| 5 |
∵四边形ABCD为平行四边形，
∴BC=AD；AD∥BC，
∴AF∥EH，△AFG∽△HEG，
∴
| AG |
| GH |
| AF |
| EH |
设AF=3λ，则DF=2λ，
∴BC=AD=5λ，代入①式得EH=2λ；
∴
| AG |
| GH |
| 3λ |
| 2λ |
| 3 |
| 5 |
∴
| AG |
| AC |
| 3 |
| 5 |
| AH |
| AC |
| 6 |
| 25 |
点评：该题主要考查了平行四边形的性质、相似三角形的判定及其性质等几何知识点及其应用问题；解题的关键是作辅助线，灵活运用平行四边形的性质、相似三角形的判定来分析、解答．
练习册系列答案
相关题目
如图，已知CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且OB=OC．
如图，将右边的图案变成左边的图案，是通过
如图，直径AE，BD交于点O，点D为
如图所示，ABCD是正方形，AE∥DB，BE=BD，BE交AD于F，试说明：△DEF是等腰三角形．
如图，AD是△ABC的高，点M在AB边上，点N在AC边上，MN⊥AD，垂足为E．下列说法正确的是
如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米．
如图，⊙O1、⊙O2外切于点P，A是⊙O1上一点，直线AC切⊙O2于点C，交⊙O1于点B，直线AP交⊙O2于点D．