题目内容
在平面直角坐标系中,O为坐标原点,点B在x轴正半轴上,且OB=2.
(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标;
(2)已知,点M(m,0)、N(0,n)(2<n<4),将点B向上平移2个单位长度后得到点B′,若∠MB′N=90°且mn=
,求m2+n2的值.
(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标;
(2)已知,点M(m,0)、N(0,n)(2<n<4),将点B向上平移2个单位长度后得到点B′,若∠MB′N=90°且mn=
| 5 |
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)利用关于直线对称的性质得出△ABO≌△ABO′,进而得出∠O′CB=90°,即可得出∠BO′C=30°,则BC=
O′B=1,即可求出点O′的横坐标;
(2)首先得出△DB′N≌△BB′M(ASA),进而得出m2+n2=(m+n)2-2mn即可得出答案.
| 1 |
| 2 |
(2)首先得出△DB′N≌△BB′M(ASA),进而得出m2+n2=(m+n)2-2mn即可得出答案.
解答: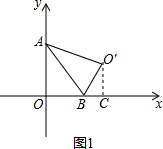 解:(1)如图1,过点O′作O′C⊥x轴,垂足为点C,
解:(1)如图1,过点O′作O′C⊥x轴,垂足为点C,
∵△ABO和△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠ABO=∠ABO′,OB=O′B=2,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=∠ABO′=60°,
∵∠OBO′+∠O′BC=180°,
∴∠O′BC=60°,
∵O′C⊥x轴,
∴∠O′CB=90°,
∴∠BO′C=30°,
∴BC=
O′B=1,
∴OC=OB+BC=3,
即点O′的横坐标为:3;
(2)如图2,
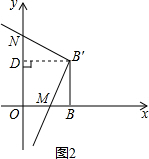
过点B′作B′D⊥y轴,垂足为点D,
∵点B在x轴正半轴上,且OB=2,
∴B(2,0),
∵点B向上平移2个单位长度后得到点B′,
∴B′(2,2),
∴BB′=B′D=2,
∵∠B′BM=90°,∠DOB=90°,∠B′DO=90°,
∴∠DB′B=90°,
∴∠DB′M+∠BB′M=90°,
∵∠MB′N=90°,
∴∠DB′M+∠DB′N=90°,
∴∠DB′N=∠BB′M,
在△DB′N和△BB′M中,
,
∴△DB′N≌△BB′M(ASA),
∴DN=BM,
∵点M(m,0),N(0,n),
∴BM=2-m,DN=n-2,
∴2-m=n-2,
即m+n=4,
∵mn=
,
∴m2+n2
=(m+n)2-2mn
=42-2
=16-2
.
 解:(1)如图1,过点O′作O′C⊥x轴,垂足为点C,
解:(1)如图1,过点O′作O′C⊥x轴,垂足为点C,∵△ABO和△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠ABO=∠ABO′,OB=O′B=2,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=∠ABO′=60°,
∵∠OBO′+∠O′BC=180°,
∴∠O′BC=60°,
∵O′C⊥x轴,
∴∠O′CB=90°,
∴∠BO′C=30°,
∴BC=
| 1 |
| 2 |
∴OC=OB+BC=3,
即点O′的横坐标为:3;
(2)如图2,

过点B′作B′D⊥y轴,垂足为点D,
∵点B在x轴正半轴上,且OB=2,
∴B(2,0),
∵点B向上平移2个单位长度后得到点B′,
∴B′(2,2),
∴BB′=B′D=2,
∵∠B′BM=90°,∠DOB=90°,∠B′DO=90°,
∴∠DB′B=90°,
∴∠DB′M+∠BB′M=90°,
∵∠MB′N=90°,
∴∠DB′M+∠DB′N=90°,
∴∠DB′N=∠BB′M,
在△DB′N和△BB′M中,
|
∴△DB′N≌△BB′M(ASA),
∴DN=BM,
∵点M(m,0),N(0,n),
∴BM=2-m,DN=n-2,
∴2-m=n-2,
即m+n=4,
∵mn=
| 5 |
∴m2+n2
=(m+n)2-2mn
=42-2
| 5 |
=16-2
| 5 |
点评:此题主要考查了全等三角形的判定与性质以及关于直线对称的性质等知识,熟练应用完全平方公式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果点C、D是线段AB上的两个点,且AC=BD,那么下列结论中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列是方程5x2-x=6的解的是( )
| A、x=1 | B、x=-1 |
| C、x=-2 | D、x=2 |
 如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F.
如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F. 如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.
如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.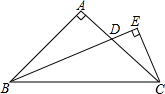 如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.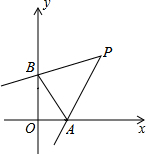 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是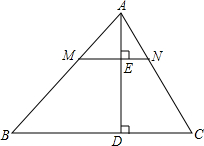 如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是
如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是