Question

2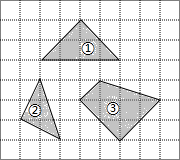．如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（　　）

• A． 只有②
• B． 只有③
• C． ②③
• D． ①②③

Answer 1

分析 利用相似三角形的判定和性质分别求出各多边形竖直部分线段长度之和与水平部分线段长度之和，再比较即可．

解答 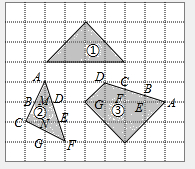解：假设每个小正方形的边长为1，
①：m=1+2+1=4，n=2+4=6，
则m≠n；
②在△ACN中，BM∥CN，
∴$\frac{BM}{CN}=\frac{AM}{AN}$=$\frac{1}{2}$，
∴BM=$\frac{1}{2}$，
在△AGF中，DM∥NE∥FG，
∴$\frac{AM}{AG}=\frac{DM}{FG}$=$\frac{1}{3}$，$\frac{AN}{AG}=\frac{NE}{FG}$=$\frac{2}{3}$，
得DM=$\frac{1}{3}$，NE=$\frac{2}{3}$，
∴m=2+$\frac{1}{2}$=2.5，n=$\frac{1}{2}$+1+$\frac{1}{3}$+$\frac{2}{3}$=2.5，
∴m=n；
③由②得：BE=$\frac{1}{3}$，CF=$\frac{2}{3}$，
∴m=2+2+$\frac{2}{3}$+1+$\frac{1}{3}$=6，n=4+2=6，
∴m=n，
则这三个多边形中满足m=n的是②和③；
故选C．

点评 本题考查了相似多边形的判定和性质，对于有中点的三角形可以利用三角形中位线定理得出；本题线段比较多要依次相加，做到不重不漏．