题目内容
10.(1)用配方法解方程:x2+4x-1=0;(2)解不等式组:$\left\{\begin{array}{l}{2x+4≤0}\\{3-2(x-1)>5}\end{array}\right.$.
分析 (1)先移项,再配方,最后直接开平方即可;
(2)先解两个不等式,再求不等式解集的公共部分即可.
解答 解:(1)移项得,x2+4x=1,
配方得,x2+4x+4=5,
即(x+2)2=5,
∴x+2=±$\sqrt{5}$,
∴x1=-2+$\sqrt{5}$,x2=-2-$\sqrt{5}$;
(2)由①得:x≤-2,
由②得:x<0,
∴不等式组的解集为x≤-2.
点评 本题考查了用配方法解一元二次方程以及解一元一次不等式组,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
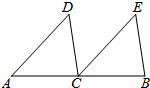
 已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).
已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).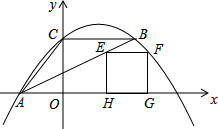 如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.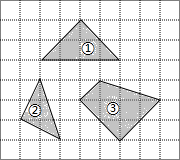 如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )