题目内容
12.关于x的方式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能是( )| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
分析 先求出x的值,再根据解为正数列出关于m的不等式,求得m的取值范围,再得出可能的m的值.
解答 解:去分母得,2x+m=3x-6,
移项合并得,x=m+6,
∵x>0,
∴m+6>0,
∴m>-6,
∵x-2≠0,
∴x≠2,
∴m+6≠2,
∴m≠-4,
∴m的取值范围为m>-6且m≠-4,
故选B.
点评 本题考查了分式方程的解,掌握解分式方程的步骤以及解为正数的条件是解题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
2. 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
7.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{(-3)^{2}}$ |
17. 如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
 如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )| A. | 70° | B. | 60° | C. | 45° | D. | 35° |
4. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )| A. | (-2,2) | B. | (4,1) | C. | (3,1) | D. | (4,0) |
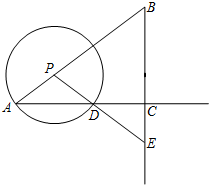 如图,在Rt△ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x.
如图,在Rt△ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x. 如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )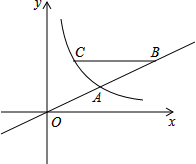 如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.