题目内容
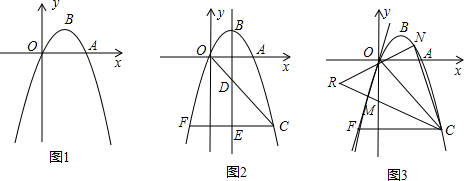
2. 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
分析 根据一次函数的性质可得∠B1OA1=45°,然后求出△OA2B2是等腰直角三角形,△OA3B2是等腰直角三角形,然后根据等腰直角三角形斜边上的高等于斜边的一半求出OA3,同理求出OA4,然后根据变化规律写出即可.
解答 解:∵直线为y=x,
∴∠B1OA1=45°,
∵△A2B2A3,
∴B2A2⊥x轴,∠B2A3A2=45°,
∴△OA2B2是等腰直角三角形,△OA3B2是等腰直角三角形,
∴OA3=2A2B2=2OA2=2×1=2,
同理可求OA4=2OA3=2×2=22,
…,
所以,OA2016=22014.
故选B.
点评 本题考查了一次函数图象上点的坐标特征,等腰直角三角形的性质,熟记性质并确定出等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.(0.125)2016×82016的值为( )
| A. | -8 | B. | 1 | C. | -4 | D. | $\frac{1}{4}$ |
10.为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查,关于酒驾设计了如下调查问卷:
随机抽取部分问卷,整理并制作了如图所示统计图:
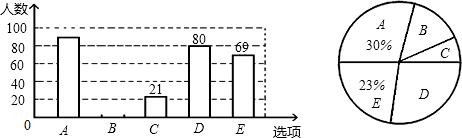
根据上述信息,解答下列问题:
(1)本次调查的司机人数是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数.
| 克服酒驾--你认为哪种方式最好?(单选) |
| A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |

根据上述信息,解答下列问题:
(1)本次调查的司机人数是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数.
7.下列性质中,菱形对角线不具有的是( )
| A. | 对角线互相垂直 | B. | 对角线所在直线是对称轴 | ||
| C. | 对角线相等 | D. | 对角线互相平分 |
14.在下面的四个几何体中,左视图与主视图不完全相同的几何是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
12.关于x的方式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能是( )
| A. | -4 | B. | -5 | C. | -6 | D. | -7 |