题目内容
4. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )| A. | (-2,2) | B. | (4,1) | C. | (3,1) | D. | (4,0) |
分析 利用网格特点和旋转的性质画出正方形ABCD绕D点顺时针旋转90°后图形,然后可写出B点旋转后的坐标.
解答 解:如图,正方形ABCD绕D点顺时针旋转90°得到正方形CB′C′D,即旋转后B点的坐标为(4,0).
故选D.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
相关题目
14.在下面的四个几何体中,左视图与主视图不完全相同的几何是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
15.“提笔忘字”正成为一个令人忧心的文化现象,为了提高中学生的汉字听写能力,我市某中学组织50名学生参加“中国梦•汉字情”中小学规范汉字听写大赛,成绩如下
这些学生成绩的中位数和众数分别是( )
| 分数/分 | 85 | 88 | 90 | 93 | 94 | 97 | 99 |
| 人数/人 | 1 | 7 | 11 | 10 | 13 | 7 | 1 |
| A. | 93分,94分 | B. | 90分,94分 | C. | 93分,93分 | D. | 94分,93分 |
12.关于x的方式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能是( )
| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
19. 如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
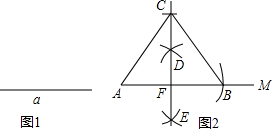 如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )| A. | AC=BC | B. | AF=BF | C. | AB=AC | D. | ∠ACF=∠BCF |
9.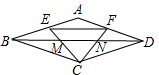 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | 3:2 |
16. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )| A. | 22° | B. | 23° | C. | 45° | D. | 68° |
13.在九龙坡区中学生初中组篮球比赛中,我校篮球队取得了全区第一名的好成绩,为了参加此次比赛,校篮球队准备购买10双运动鞋,各种尺码的统计如表所示,则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5 26 | B. | 26 25.5 | C. | 26 26 | D. | 25.5 25.5 |
 某中学为了解该校学生一年的课外阅读量,随机抽取了n名学生进行调查,并将调查结果绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
某中学为了解该校学生一年的课外阅读量,随机抽取了n名学生进行调查,并将调查结果绘制成如下条形统计图,根据统计图提供的信息解答下列问题: