题目内容
1.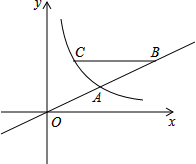 如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.(1)求反比例函数的解析式;
(2)如果点B在直线y=$\frac{1}{2}$x上,点C在反比例函数图象上,BC∥x轴,BC=3,且BC在点A上方,求点B的坐标.
分析 (1)把x=2代入y=$\frac{1}{2}$x得出点A坐标,从而求得反比例函数的解析式;
(2)设点C($\frac{2}{m}$,m),根据BC∥x轴,得点B(2m,m),再由BC=3,列出方程求得m,检验得出答案.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$(k≠0),
∵横坐标为2的点A在直线y=$\frac{1}{2}$x上,∴点A的坐标为(2,1),
∴1=$\frac{k}{2}$,
∴k=2,
∴反比例函数的解析式为$\frac{2}{x}$;
(2)设点C($\frac{2}{m}$,m),则点B(2m,m),
∴BC=2m-$\frac{2}{m}$=3,
∴2m2-3m-2=0,
∴m1=2,m2=-$\frac{1}{2}$,
m1=2,m2=-$\frac{1}{2}$都是方程的解,但m=-$\frac{1}{2}$不符合题意,
∴点B的坐标为(4,2).
点评 本题考查了反比例函数和一次函数的交点问题,掌握待定系数法求解析式以及平行于坐标轴上两点间距离的求法是解题的关键.

练习册系列答案
相关题目
12.关于x的方式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能是( )
| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
9.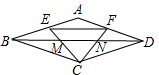 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | 3:2 |
16. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )| A. | 22° | B. | 23° | C. | 45° | D. | 68° |
6.下列计算正确的是( )
| A. | 2-1=-2 | B. | $\sqrt{9}$=±3 | C. | (a4)3=a7 | D. | -(3pq)2=-9p2q2 |
13.在九龙坡区中学生初中组篮球比赛中,我校篮球队取得了全区第一名的好成绩,为了参加此次比赛,校篮球队准备购买10双运动鞋,各种尺码的统计如表所示,则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5 26 | B. | 26 25.5 | C. | 26 26 | D. | 25.5 25.5 |
 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.