题目内容
2.如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤1,1<x≤m,m<x≤3时,函数的解析式不同)(1)填空:BC的长是3;
(2)求S关于x的函数关系式,并写出x的取值范围.

分析 (1)由图象即可解决问题.
(2)分三种情形①如图1中,当0≤x≤1时,作DM⊥AB于M,根据S=S△ABC-S△BDF-S四边形ECAG即可解决.
②如图2中,作AN∥DF交BC于N,设BN=AN=x,在RT△ANC中,利用勾股定理求出x,再根据S=S△ABC-S△BDF-S四边形ECAG即可解决.
③如图3中,根据S=$\frac{1}{2}$CD•CM,求出CM即可解决问题.
解答 解;(1)由图象可知BC=3.
故答案为3.
(2)①如图1中,当0≤x≤1时,作DM⊥AB于M,
由题意BC=3,AC=2,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{13}$,
∵∠B=∠B,∠DMB=∠C=90°,
∴△BMD∽△BCA,
∴$\frac{DM}{AC}$=$\frac{BM}{BC}$=$\frac{DB}{AB}$,
∴DM=$\frac{2x}{\sqrt{13}}$,BM=$\frac{3x}{\sqrt{13}}$,
∵BD=DF,DM⊥BF,
∴BM=MF,
∴S△BDF=$\frac{6}{13}$x2,
∵EG∥AC,
∴$\frac{EG}{AC}$=$\frac{BE}{BC}$,
∴$\frac{EG}{2}$=$\frac{x+2}{3}$,
∴EG=$\frac{2}{3}$(x+2),
∴S四边形ECAG=$\frac{1}{2}$[2+$\frac{2}{3}$(x+2)]•(1-x),
∴S=S△ABC-S△BDF-S四边形ECAG=3-$\frac{6}{13}$x2-$\frac{1}{2}$[2+$\frac{2}{3}$(x+2)]•(1-x)=-$\frac{5}{39}$x2+$\frac{4}{3}$x+$\frac{4}{3}$.
②如图②中,作AN∥DF交BC于N,设BN=AN=x,
在RT△ANC中,∵AN2=CN2+AC2,
∴x2=22+(3-x)2,
∴x=$\frac{13}{6}$,
∴当1<x≤$\frac{13}{6}$时,S=S△ABC-S△BDF=3-$\frac{6}{13}$x2,
③如图3中,当$\frac{13}{6}$<x≤3时,
∵DM∥AN,
∴$\frac{CD}{CN}$=$\frac{CM}{CA}$,
∴$\frac{3-x}{3-\frac{13}{6}}$=$\frac{CM}{2}$,
∴CM=$\frac{12}{5}$(3-x),
∴S=$\frac{1}{2}$CD•CM=$\frac{6}{5}$(3-x)2,
综上所述S=$\left\{\begin{array}{l}{-\frac{5}{39}{x}^{2}+\frac{4}{3}x+\frac{4}{3}}&{(0≤x≤1)}\\{3-\frac{6}{13}{x}^{2}}&{(1<x≤\frac{13}{6})}\\{\frac{6}{5}(3-x)^{2}}&{(\frac{13}{6}<x≤3)}\end{array}\right.$.
点评 本题考查四边形综合题、等腰三角形的性质、相似三角形的性质、勾股定理等知识,解题的关键是学会分类讨论,正确画出图形,属于中考压轴题.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5 26 | B. | 26 25.5 | C. | 26 26 | D. | 25.5 25.5 |
| 阅读时间(小时) | 1 | 2 | 3 | 4 | 5 |
| 人数(人) | 6 | 17 | 16 | 6 | 5 |
| A. | 17,16 | B. | 17,17 | C. | 6,16 | D. | 2,3 |
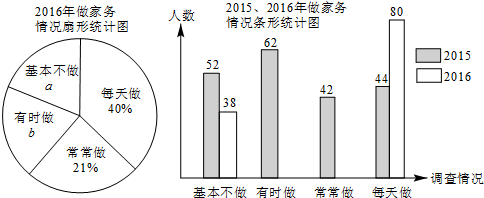
 某中学为了解该校学生一年的课外阅读量,随机抽取了n名学生进行调查,并将调查结果绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
某中学为了解该校学生一年的课外阅读量,随机抽取了n名学生进行调查,并将调查结果绘制成如下条形统计图,根据统计图提供的信息解答下列问题: 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.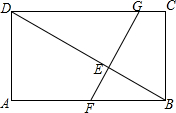 如图,在矩形ABCD中,AB=9,AD=3$\sqrt{3}$,E为对角线BD上一点,且DE=2BE,过E作FG⊥BD,分别交AB、CD于F、G.将四边形BCGF绕点B旋转180°,在此过程中,设直线GF分别与直线CD、BD交于点M、N,当△DMN是以∠MDN为底角的等腰三角形时,则DN的长是10$\sqrt{3}$或6$\sqrt{3}$-4.
如图,在矩形ABCD中,AB=9,AD=3$\sqrt{3}$,E为对角线BD上一点,且DE=2BE,过E作FG⊥BD,分别交AB、CD于F、G.将四边形BCGF绕点B旋转180°,在此过程中,设直线GF分别与直线CD、BD交于点M、N,当△DMN是以∠MDN为底角的等腰三角形时,则DN的长是10$\sqrt{3}$或6$\sqrt{3}$-4.