题目内容

17．如图，AB为⊙O的直径，点C在⊙O上，连接AC，OC，过点B作BD⊥OC，交⊙O于点D，已知∠ACO=35°，则∠COD的度数为（　　）
A．70°B．60°C．45°D．35°

分析 根据等腰三角形的性质得到∠OAC=∠ACO=35°，由圆周角定理得到∠BOC=2∠A=70°，根据垂径定理即可得到结论．

解答 解：∵OA=OC，
∴∠OAC=∠ACO=35°，
∴∠BOC=2∠A=70°，
∵BD⊥OC，
∴$\widehat{CD}$=$\widehat{BC}$，
∴∠COD=∠BOC=70°．
故选A．

点评 本题考查了圆周角定理，垂径定理，熟练掌握圆周角定理是解题的关键．

练习册系列答案
相关题目
7．下列性质中，菱形对角线不具有的是（　　）
A．对角线互相垂直B．对角线所在直线是对称轴
C．对角线相等D．对角线互相平分
8．如图所示，已知AB∥CD，直线EF交AB于点E，交CD于点F，且EG平分∠FEB，∠1=60°，则∠2等于（　　）
A．40°B．45°C．50°D．60°
5．下列运算，正确的是（　　）
A．4a-2a=2B．a6÷a3=a2C．（$\frac{1}{2}$）-1-22=-2D．（a-b）2=a2-b2
12．关于x的方式方程$\frac{2x+m}{x-2}$=3的解是正数，则m可能是（　　）
A．-4B．-5C．-6D．-7
2．如图所示，下列各组角的位置，判断错误的是（　　）
A．∠C和∠CFG是同旁内角B．∠CGF和∠AFG是内错角
C．∠BGF和∠A是同旁内角D．∠BGF和∠AFD是同位角
9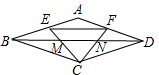．如图，在菱形ABCD中，点E、F分别是边AB、AD的中点，连接CE、CF交对角线BD于点M、N，连接EF，则BN：EF等于（　　）
A．1：1B．1：2C．2：3D．3：2
6．下列计算正确的是（　　）
A．2-1=-2B．$\sqrt{9}$=±3C．（a4）3=a7D．-（3pq）2=-9p2q2
7．每年4月23日是“世界读书日”，某校为了了解学生课外书的阅读情况，对该校九年一班50名学生一周阅读课外书的时间进行了统计，统计结果如下：由表知，这50名学生一周阅读课外书的时间的众数和中位数分别为（　　）
阅读时间（小时）12345
人数（人）6171665
A．17，16B．17，17C．6，16D．2，3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网