题目内容
17.先化简,再求值:(1)6a2-(2a-1)(3a+2)+(a+2)(a-2),其中a=-$\sqrt{2}$
(2)$\frac{x-3}{2x-4}$÷($\frac{5}{x-2}$-x-2),其中x=$\sqrt{3}$-3.
分析 (1)先去括号,再合并同类项,代入a的值计算即可;
(2)先算括号里面的,再约分,代入x的值计算即可.
解答 接:(1)原式=6a2-6a2-4a+3a+2+a2-2a+2a-4,
=a2-a-2,
当a=-$\sqrt{2}$时,原式=${(-\sqrt{2})^2}-(-\sqrt{2})-2=\sqrt{2}$;
(2)原式=$\frac{x-3}{2x-4}$÷($\frac{5}{x-2}$-$\frac{{x}^{2}-4}{x-2}$),
=$\frac{x-3}{2x-4}$÷$\frac{9-{x}^{2}}{x-2}$
=$\frac{x-3}{2(x-2)}$•$\frac{x-2}{(3+x)(3-x)}$
=$-\frac{1}{2x+6}$,
当x=$\sqrt{3}$-3时,原式=$-\frac{1}{{2(\sqrt{3}-3)+6}}=-\frac{1}{{2\sqrt{3}}}=-\frac{{\sqrt{3}}}{6}$.
点评 本题考查了分式的化简求值,掌握运算法则是解题的关键.

练习册系列答案
相关题目
2.二元一次方程2x+3y=18的正整数解共有多少组( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.下面各图中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
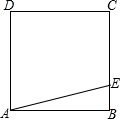 有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.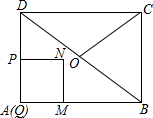 如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).