题目内容
5.求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,S=22015-1,我们把这种求和的方法叫错位相加减,仿照上述的思路方法,计算出1+5+52+53+…+52014的值为( )| A. | 52014-1 | B. | 52015-1 | C. | $\frac{{5}^{2015}-1}{4}$ | D. | $\frac{{5}^{2014}-1}{4}$ |
分析 根据题目信息,设S=1+5+52+53+…+52014,表示出5S=5+52+53+…+52015,然后相减求出S即可..
解答 解:设S=1+5+52+53+…+52014,
则5S=5+52+53+…+52015,
5S-S=(5+52+53+…+52015)-(1+5+52+53+…+52014)=52015-1,
所以,S=$\frac{{5}^{2015}-1}{4}$.
故选:C.
点评 本题考查了整式的混合运算,读懂题目信息,理解等比数列的求和方法是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.一次函数y=-x+2图象经过( )象限.
| A. | 一、二、三 | B. | 一、二、四 | C. | 一、三、四 | D. | 二、三、四 |
20.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对某班50名同学体重情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对闽江水质情况的调查 | |
| D. | 对某类烟花爆竹燃放安全情况的调查 |
14. 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )| A. | 110° | B. | 80° | C. | 55° | D. | 35° |
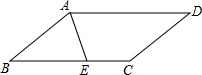 已知:如图,在?ABCD中,AE平分∠BAD,交BC于点E.
已知:如图,在?ABCD中,AE平分∠BAD,交BC于点E. …,请仔细观察,按此规律在前8个图案中有2个
…,请仔细观察,按此规律在前8个图案中有2个 ,按此规律在前15个图案中有4个
,按此规律在前15个图案中有4个 ,按此规律在前2015个图案中有503个
,按此规律在前2015个图案中有503个