题目内容
5．
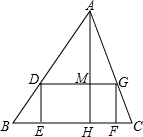如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，（1）求y关于x的函数关系式；
（2）当x为何值时，四边形DEFG的面积最大？最大面积是多少？
分析 （1）设DE=y，则MH=y，AM=AH-MH=8-y，因为DG∥BC，可证△ADG∽△ABC，根据相似三角形对应边上高的比等于相似比，建立等式；
（2）设四边形DEFG的面积为S，则S=DE×DG=xy=x（8-$\frac{4}{5}$x），运用二次函数性质解决问题．
解答 解：（1）设AH与DG交于点M，则AM=AH-MH=8-y，
∵DG∥BC，∴△ADG∽△ABC，
∴$\frac{AM}{AH}$=$\frac{DG}{BC}$，即$\frac{8-y}{8}=\frac{x}{10}$，
整理，得$y=8-\frac{4}{5}x$；
（2）设四边形DEFG的面积为S，则S=DE×DG=xy=x（8-$\frac{4}{5}$x）=-$\frac{4}{5}{x}^{2}$+8x，
当x=-$\frac{b}{2a}$=5时，S=-$\frac{4}{5}$×25+8×5=20，
所以当x=5时，四边形DEFG面积最大，最大面积是20．
点评 本题考查了相似三角形的应用，二次函数的最值问题，根据相似三角形的对应高的比等于相似比用矩形DEFG的宽表示出长是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，∠BAC=90°，∠B=60°，AD⊥BC于点D，则△ABD与△ADC的面积比为1：3．
已知：线段a，b和c（如图），用直尺和圆规作△ABC，使BC=a，CA=b，AB=c．（请保留作图痕迹，不写作法）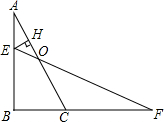
如图，在直角三角形ABC中，点E在线段AB上，过点E作EH⊥AC交AC于点H，点F在BC的延长线上，连结EF交AC于点O．若AB=2，BC=1，且$\frac{CF}{AE}=2$，则$\frac{OE}{OF}$=$\frac{1}{4}$，OH=$\frac{\sqrt{5}}{5}$．
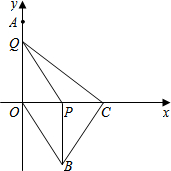如图，在平面直角坐标系中，点A （0，4）．动点P从原点O出发，沿x轴正方向以每秒2个单位的速度运动，同时动点Q从点A出发，沿y轴负方向以每秒1个单位的速度运动，以QO、QP为邻边构造平行四边形OQPB，在线段OP的延长线长取点C，使得PC=2，连接BC、CQ．设点P运动的时间为t（0＜t＜4）秒．