Question

7．将长为8cm，宽为6cm的矩形纸片ABCD折叠，使A与C重合，则折痕的长为（　　）

• A． 6.5cm
• B． 7cm
• C． 7.5cm
• D． 8cm

Answer 1

分析 先根据题意画出图形，然后连接AC，由勾股定理可求得AC的长，然后由翻折的性质可求得AO=$\frac{1}{2}$AC，接下来证明△AOE∽△ABC，由相似三角形的性质可求得的长，同理可求得OF的长，于是可求得折痕EF的长．

解答 解：如图所示：连接AC．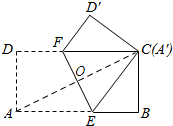

∵AB=8，BC=6，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10．
由翻折的性质可知：AO=OC=5．
∵∠OAE=∠CAB，∠EOA=∠ABC=90°，
∴△AOE∽△ABC．
∴$\frac{AO}{AB}=\frac{OE}{BC}$，即$\frac{5}{8}=\frac{OE}{6}$，解得OE=$\frac{15}{4}$．
同理；OF=$\frac{15}{4}$．
∴EF=2×$\frac{15}{4}$=7.5．
故选：C．

点评 本题主要考查的是翻折的性质、勾股定理、相似三角形的性质和判定，依据相似三角形的性质求得OE、OF的长是解题的关键．