题目内容
选择适当的方法解下列方程:
(1)x2-3x=0
(2)(2x-5)2-(x+4)2=0
(3)x2-2x-8=0
(4)(x+1)(x+2)=2x+4
(5)3(x-2)2=x2-4
(6)x2+2x-143=0.
(1)x2-3x=0
(2)(2x-5)2-(x+4)2=0
(3)x2-2x-8=0
(4)(x+1)(x+2)=2x+4
(5)3(x-2)2=x2-4
(6)x2+2x-143=0.
考点:解一元二次方程-因式分解法
专题:计算题
分析:(1)利用因式分解法解方程;
(2)利用因式分解法解方程;
(3)利用因式分解法解方程;
(4)先变形为(x+1)(x+2)-2(x+2)=0,再利用因式分解法解方程;
(5)先变形为3(x-2)2-(x+2)(x-2)=0,再利用因式分解法解方程;
(6)利用因式分解法解方程.
(2)利用因式分解法解方程;
(3)利用因式分解法解方程;
(4)先变形为(x+1)(x+2)-2(x+2)=0,再利用因式分解法解方程;
(5)先变形为3(x-2)2-(x+2)(x-2)=0,再利用因式分解法解方程;
(6)利用因式分解法解方程.
解答:解:(1)x(x-3)=0,
所以x1=0,x2=3;
(2)(2x-5+x+4)(2x-5-x-4)=0,
2x-5+x+4=0或2x-5-x-4=0,
所以x1=
,x2=9;
(3)(x-4)(x+2)=0,
所以x1=,4,x2=-2;
(4)(x+1)(x+2)-2(x+2)=0,
(x+2)(x+1-2)=0,
所以x1=-2,x2=1;
(5)3(x-2)2-(x+2)(x-2)=0,
(x-2)(3x-6-x-2)=0,
x-2=0或3x-6-x-2=0,
所以x1=2,x2=4;
(6)(x+13)(x-11)=0,
所以x1=-13,x2=11.
所以x1=0,x2=3;
(2)(2x-5+x+4)(2x-5-x-4)=0,
2x-5+x+4=0或2x-5-x-4=0,
所以x1=
| 1 |
| 3 |
(3)(x-4)(x+2)=0,
所以x1=,4,x2=-2;
(4)(x+1)(x+2)-2(x+2)=0,
(x+2)(x+1-2)=0,
所以x1=-2,x2=1;
(5)3(x-2)2-(x+2)(x-2)=0,
(x-2)(3x-6-x-2)=0,
x-2=0或3x-6-x-2=0,
所以x1=2,x2=4;
(6)(x+13)(x-11)=0,
所以x1=-13,x2=11.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.

练习册系列答案
相关题目
 如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?
如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?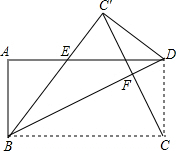 如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E.
如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E.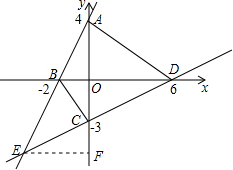 已知直线m经过两点(1,6)、(-3,-2),它和x轴、y轴的交点式B、A,直线n过点(2,-2),且与y轴交点的纵坐标是-3,它和x轴、y轴的交点是D、C;
已知直线m经过两点(1,6)、(-3,-2),它和x轴、y轴的交点式B、A,直线n过点(2,-2),且与y轴交点的纵坐标是-3,它和x轴、y轴的交点是D、C; 在?ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
在?ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.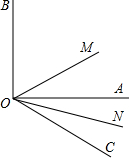 已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线.
已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线.