题目内容
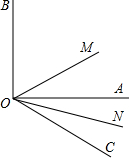 已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线.
已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线.(1)若∠AOB=90°,∠AOC=30°,求∠MON的大小.
(2)若∠AOB=α,∠AOC=β,试用含α,β的代数式表示∠MON,并直接写出∠MON与∠BOC的倍数关系.
考点:角的计算,角平分线的定义
专题:常规题型
分析:由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可.
解答:解:(1)∵ON是∠AOC的平分线,且∠AOC=30°,
∴∠NOA=
∠AOC=15°,
∵OM是∠AOB的平分线,且∠AOB=90°,
∴∠MOA=
∠AOB=45°,
∵∠MON=∠NOA+∠MOA,
∴∠MON=15°+45°=60°.
(2))∵ON是∠AOC的平分线,且∠AOC=β,
∴∠NOA=
∠AOC=
β,
∵OM是∠AOB的平分线,且∠AOB=α,
∴∠MOA=
∠AOB=
α,
∵∠MON=∠NOA+∠MOA,
∴∠MON=
β+
α.
由∠MON=
β+
α,
∴∠MON=
(β+α)=
(∠AOB+∠AOC)=
∠BOC\.
即:∠BOC=2∠MON.

∴∠NOA=
| 1 |
| 2 |
∵OM是∠AOB的平分线,且∠AOB=90°,
∴∠MOA=
| 1 |
| 2 |
∵∠MON=∠NOA+∠MOA,
∴∠MON=15°+45°=60°.
(2))∵ON是∠AOC的平分线,且∠AOC=β,
∴∠NOA=
| 1 |
| 2 |
| 1 |
| 2 |
∵OM是∠AOB的平分线,且∠AOB=α,
∴∠MOA=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠MON=∠NOA+∠MOA,
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
由∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即:∠BOC=2∠MON.

点评:本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠MOA和∠NOA的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 画出下列几何体的三视图.
画出下列几何体的三视图.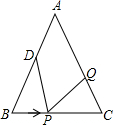 如图,已△ABC中,AB=AC=12厘米,BC=9厘,点D为AB的中点.
如图,已△ABC中,AB=AC=12厘米,BC=9厘,点D为AB的中点.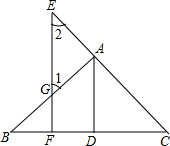 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.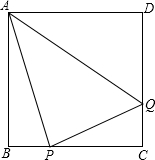 如图,在边长为4的正方形ABCD中,动点P从点B出发沿BC向点C运动,动点Q同时以相同的速度从点C出发沿CD向D点运动.
如图,在边长为4的正方形ABCD中,动点P从点B出发沿BC向点C运动,动点Q同时以相同的速度从点C出发沿CD向D点运动.