题目内容
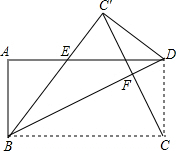 如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E.
如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E.(1)图中的△
(2)直接写出图中所有的三角形;
(3)若AD=4,AB=3,BD=5,连接CC′交BD于F,试求出CC′的大小.
考点:翻折变换(折叠问题)
专题:计算题
分析:(1)根据折叠的性质可判断△BC′D和△BCD关于直线BD成轴对称;
(2)共有6个三角形;
(3)先得到BC=AD=4,CD=AB=3,则根据轴对称的性质得CF⊥BD,CC′=2CF,然后利用面积法计算出CF的长,再由CC′=2CF计算即可.
(2)共有6个三角形;
(3)先得到BC=AD=4,CD=AB=3,则根据轴对称的性质得CF⊥BD,CC′=2CF,然后利用面积法计算出CF的长,再由CC′=2CF计算即可.
解答:解:(1)∵四边形ABCD沿着BD折叠,使点C落在C′处,
∴△BC′D和△BCD关于直线BD成轴对称;
故答案为BC′D,BCD,直线BD;
(2)图中的三角形有:△ABD、△BCD、△BC′D、△ABE、△BDE、△DEC′;
(3)∵AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°,
∴BC=AD=4,CD=AB=3,
∵△BC′D和△BCD关于直线BD成轴对称,
∴BD垂直平分CC′,即CF⊥BD,CC′=2CF,
∵
CF•BD=
BC•CD,
∴CF=
=
,
∴CC′=
.
∴△BC′D和△BCD关于直线BD成轴对称;
故答案为BC′D,BCD,直线BD;
(2)图中的三角形有:△ABD、△BCD、△BC′D、△ABE、△BDE、△DEC′;
(3)∵AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°,
∴BC=AD=4,CD=AB=3,
∵△BC′D和△BCD关于直线BD成轴对称,
∴BD垂直平分CC′,即CF⊥BD,CC′=2CF,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴CC′=
| 24 |
| 5 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质.

练习册系列答案
相关题目
 如图,已知AB=AC,BD=CD,试用“边边边”识别法说明:∠B=∠C.
如图,已知AB=AC,BD=CD,试用“边边边”识别法说明:∠B=∠C. 如图,已知AD、BE是△ABC的高,AD、BE相交于点F,并且AD=BD,你能找到图中的全等三角形吗?若能找到请说明理由.
如图,已知AD、BE是△ABC的高,AD、BE相交于点F,并且AD=BD,你能找到图中的全等三角形吗?若能找到请说明理由.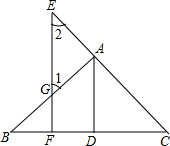 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2. 实数a在数轴上的位置如图所示,化简:
实数a在数轴上的位置如图所示,化简: