题目内容
2.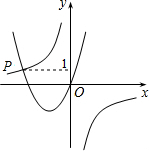 已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.
已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.
分析 根据点P的纵坐标利用反比例函数图象上点的坐标特征即可求出点P的坐标,观察函数图象的上下位置关系即可得出不等式的解.
解答 解:当y=1时,有-$\frac{2}{x}$=1,
解得:x=-2,
∴点P的坐标为(-2,1).
原不等式可变形为:ax2-bx>-$\frac{2}{x}$,
观察函数图象可知:当x<-2或x>0时,抛物线在双曲线的上方,
∴关于x的不等式ax2+$\frac{2}{x}$>bx的解为x<-2或x>0.
故答案为:x<-2或x>0.
点评 本题考查了反比例函数图象上点的坐标特征,根据函数图象的上下位置关系找出不等式的解集是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.抛物线y=(x-m)2+n可以由抛物线y=x2向上平移2个单位,再向左平移3个单位得到,则m-n值为( )
| A. | -6 | B. | -5 | C. | -1 | D. | 1 |
14.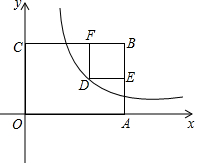 如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
 如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )| A. | (2,6) | B. | (3,4) | C. | (4,3) | D. | (6,2) |
