题目内容
14.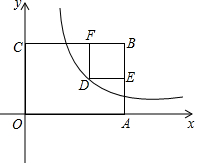 如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=$\frac{12}{x}$上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )| A. | (2,6) | B. | (3,4) | C. | (4,3) | D. | (6,2) |
分析 由点D在双曲线上可设点D的坐标为(m,$\frac{12}{m}$)(m>0),根据点B的坐标即可得出DE、DF的长度,根据正方形的性质即可得出关于m的分式方程,解之经检验后即可得出结论.
解答 解:∵点D在双曲线y=$\frac{12}{x}$上,
∴设点D的坐标为(m,$\frac{12}{m}$)(m>0),
∵B(7,6),
∴DE=7-m,DF=6-$\frac{12}{m}$,
∵四边形DEBF为正方形,
∴7-m=6-$\frac{12}{m}$,
解得:m=4或m=-3(舍去),
经检验x=4是方程7-m=6-$\frac{12}{m}$的解,
∴点D的坐标为(4,3).
故选C.
点评 本题考查了反比例函数图象上点的坐标特征以及正方形的性质,根据正方形的性质找出关于m的分式方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知a、b、c为实数,且(a-c)2>a2+c2,则关于x的方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 无实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有一根为0 |
6.在-$\frac{1}{2}$,-$\frac{1}{3}$,-2,-1这四个数中,最大的数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
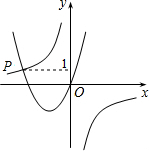 已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.
已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.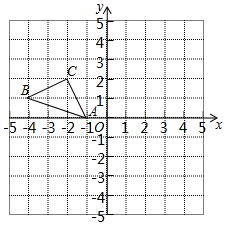 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: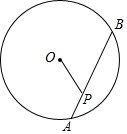 如图,圆O的直径为10cm,弦AB的长为8cm,P是弦AB上一点,若OP的长是整数,则满足条件的点P有几个( )
如图,圆O的直径为10cm,弦AB的长为8cm,P是弦AB上一点,若OP的长是整数,则满足条件的点P有几个( ) 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.