题目内容
11.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:(1)数轴上表示2和5的两点之间的距离是3,数轴上表示2和-3的两点之间的距离是5.
(2)数轴上表示x和-2的两点之间的距离表示为|x+2|.
(3)若x表示一个有理数,且-4≤x≤-2,则|x-2|+|x+4|=6.
(4)若|x+3|+|x-5|=8,利用数轴求出x的整数值.
分析 (1)根据数轴上两点间的距离是大数减小数,可得答案;
(2)根据数轴上两点间的距离是大数减小数,可得答案;
(3)根据线段上的点到线段的两端点的距离的和等于线段的距离,可得答案;
(4)根据线段上的点到线段的两端点的距离的和等于线段的距离,可得答案.
解答  解:(1)数轴上表示2和5两点之间的距离是5-2=3,数轴上表示2和-3的两点之间的距离是2-(-3)=5;
解:(1)数轴上表示2和5两点之间的距离是5-2=3,数轴上表示2和-3的两点之间的距离是2-(-3)=5;
(2)数轴上表示x和-2的两点之间的距离表示为|x+2|;
(3)若x表示一个有理数,且-4≤x≤-2,则|x-2|+|x+4|=6; (4)∵|x+3|+|x-5|=8,
(4)∵|x+3|+|x-5|=8,
∴-3≤x≤5,
∵x为整数,
∴x=-3,-2,-1,0,1,2,3,4,5.
故答案为:3,5;|x+2|;6.
点评 本题考查了整式的加减,数轴,利用了两点间的距离公式,线段上的点到线段的两端点的距离的和等于线段的距离.

练习册系列答案
相关题目
6.在-$\frac{1}{2}$,-$\frac{1}{3}$,-2,-1这四个数中,最大的数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
20.某服装店新开张,第一天销售服装a件,第二天比第一天多销售12件,第三天的销售量是第二天的2倍少14件,则第三天销售了( )
| A. | (2a+2)件 | B. | (2a+20)件 | C. | (2a+10)件 | D. | (2a-10)件 |
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是27cm2,AB=10cm,AC=8cm.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是27cm2,AB=10cm,AC=8cm.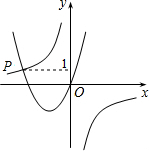 已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.
已知函数y=$\frac{-2}{x}$与y=ax2-bx(a>0,b<0)的图象交于点P,点P的纵坐标为1.则关于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.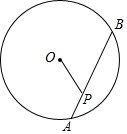 如图,圆O的直径为10cm,弦AB的长为8cm,P是弦AB上一点,若OP的长是整数,则满足条件的点P有几个( )
如图,圆O的直径为10cm,弦AB的长为8cm,P是弦AB上一点,若OP的长是整数,则满足条件的点P有几个( )