题目内容
17.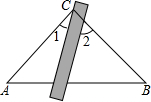 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
分析 根据两条平行线被第三条直线所截,同位角相等,可得∠3=∠2=55°,然后用90°减去∠3的度数,求出∠1的度数等于多少即可.
解答 解:如图,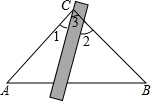 ,
,
∵两条平行线被第三条直线所截,同位角相等,
∴∠3=∠2=55°,
又∵∠1+∠3=∠ACB=90°,
∴∠1=90°-55°=35°,
即∠1的度数等于35°.
故选:D.
点评 此题主要考查了平行线性质定理,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.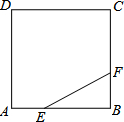 如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
 如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )| A. | 12 | B. | 9 | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
7.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).
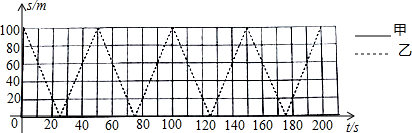
(2)根据(1)中所画图象,完成下列表格:
(3)①直接写出甲、乙两人分别在第一个100m内,t与s的函数解析式,并指出自变量t的取值范围.
②求甲、乙第6次相遇时t的值.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).

(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②求甲、乙第6次相遇时t的值.
 如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.
如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.
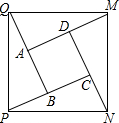 如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.
如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.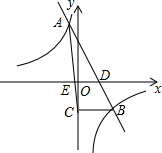 一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.
一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D. 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.