题目内容
6. 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.
分析 (1)证明△OMP≌△ONP,即可证得MN⊥OT,且OT平分MN;
(2)①若经过A,B,C,D四个点的圆存在,则对角互补,据此即可判断;
②已知FM⊥AB,作EG⊥AB于G,根据菱形的面积公式求得GE的长,然后根据△BNE∽△BFD求得BF的长,再根据△BEG∽△BFM求得FM的长.
解答 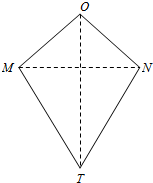 解:(1)猜想:筝形对角线之间的位置关系:垂直.即OT⊥MN.
解:(1)猜想:筝形对角线之间的位置关系:垂直.即OT⊥MN.
证明:连接OT,MN,
在△OMT和△ONT中,
$\left\{\begin{array}{l}{OM=ON}\\{OT=OT}\\{TM=TN}\end{array}\right.$,
∴△OMT≌△ONT(SSS),
∴∠MOT=∠NOT,
∵OM=ON,
∴OT⊥MN(等腰三角形三线合一).
(2)①存在.
由(1)得AC⊥BD,设AC与BD交于点M,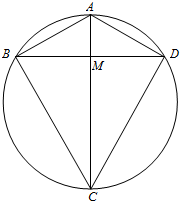
在Rt△AMB中,AB=5,BM=$\frac{1}{2}$BD=4,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3,
∵A、B、C、D四点共圆,
∴∠ABC+∠ADC=180°,
又∵△ABC≌△ADC,
∴∠ABC=∠ADC=90°,
∴AC即为所求圆的直径
∵∠BAM=∠BAC,∠ABC=∠AMB=90°,
∴△ABM∽△ACB,
∴$\frac{AB}{AC}$=$\frac{AM}{AB}$,即$\frac{5}{AC}$=$\frac{3}{5}$,
∴AC=$\frac{25}{3}$
∴圆的半径为:$\frac{1}{2}$AC=$\frac{25}{6}$.
②作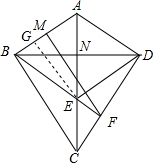 FM⊥AB,作EG⊥AB于G.
FM⊥AB,作EG⊥AB于G.
∵四边形ABED是菱形,
∴AE⊥BD,且BN=$\frac{1}{2}$BD=4,
∴AN=NE=$\sqrt{A{B}^{2}-B{N}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,AE=6.
∴S菱形ABED=$\frac{1}{2}$AE•BD=$\frac{1}{2}$×6×8=24,
又∵S菱形ABED=AB•EG,
∴EG=$\frac{24}{5}$.
∵∠DBF=∠DBF,∠BNE=∠BFD,
∴△BNE∽△BFD,
∴$\frac{BF}{BN}=\frac{BD}{BE}$,即$\frac{BF}{4}=\frac{8}{5}$,
∴BF=$\frac{32}{5}$.
∵GE⊥AB,FM⊥AB,
∴GE∥FM,
∴△BEG∽△BFM,
∴$\frac{FM}{GE}=\frac{BF}{BE}$,即$\frac{FM}{\frac{24}{5}}=\frac{\frac{32}{5}}{5}$,
解得:FM=$\frac{768}{125}$.
点评 本题考查了菱形的判定与性质,以及相似三角形的判定与性质,正确作出辅助线是关键,在初中范围内求线段长的基本方法是解直角三角形和利用三角形相似求解.

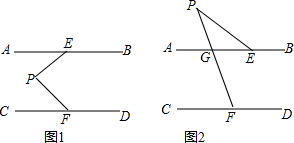
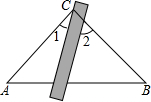 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
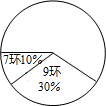 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
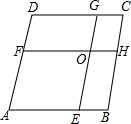 如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )| A. | 6.5 | B. | 6 | C. | 5.5 | D. | 5 |
 如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 236π | B. | 136π | C. | 132π | D. | 120π |
 如图所示的几何体的左视图为( )
如图所示的几何体的左视图为( )| A. |  | B. |  | C. |  | D. |  |
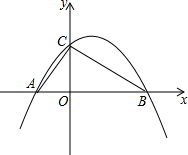 如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.